Graphs




Next: The cycle type
Up: Actions
Previous: Enumeration of symmetry
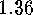 .
.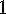 Example
We would like to derive from
Example
We would like to derive from  a formula for the number of
graphs on
a formula for the number of
graphs on  vertices. Before we start doing so it should be mentioned
that this example is the second typical example which we present.
The first
examples
were devoted to the
introduction of group theoretical concepts,
to
the derivation of Sylow's Theorem
and to a
number theoretic result of Fermat.
The only example where a suitable choice of
vertices. Before we start doing so it should be mentioned
that this example is the second typical example which we present.
The first
examples
were devoted to the
introduction of group theoretical concepts,
to
the derivation of Sylow's Theorem
and to a
number theoretic result of Fermat.
The only example where a suitable choice of  and
and 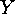 was made in order to define and enumerate a mathematical structure
was in fact
the composition of two symmetric groups.
As this example
may have been a little bit artificial we admit that it is
only now that we start to apply our paradigmatic actions more systematically.
Let us see how suitably chosen
was made in order to define and enumerate a mathematical structure
was in fact
the composition of two symmetric groups.
As this example
may have been a little bit artificial we admit that it is
only now that we start to apply our paradigmatic actions more systematically.
Let us see how suitably chosen  ,
, 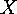 and
and 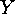 can be used in order to define
and enumerate the graphs on
can be used in order to define
and enumerate the graphs on  vertices.(Later on we shall refine this method
by counting these graphs according to the number of edges or according
to their automorphism group. Finally we shall even use this Ansatz
in order to construct such graphs and also to generate them
uniformly at random.) The way of defining
graphs as orbits of groups may at first glance seem to be circumstantial,
but we shall see that this definition is very flexible since it can easily be
generalized to all other kinds of graphs like multigraphs, directed graphs
and so on.
vertices.(Later on we shall refine this method
by counting these graphs according to the number of edges or according
to their automorphism group. Finally we shall even use this Ansatz
in order to construct such graphs and also to generate them
uniformly at random.) The way of defining
graphs as orbits of groups may at first glance seem to be circumstantial,
but we shall see that this definition is very flexible since it can easily be
generalized to all other kinds of graphs like multigraphs, directed graphs
and so on.
- A labelled (simple) graph
consists
of a set of vertices and
a set of edges
joining pairs of vertices, but neither loops
(i.e. edges joining a vertex with itself) nor multiple edges are allowed.
Thus a labelled graph on
 vertices can be considered (after numbering the
vertices from 1 to
vertices can be considered (after numbering the
vertices from 1 to  , say) as a map
, say) as a map 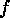 from the set
from the set
 of
(unordered) pairs of vertices into the set
of
(unordered) pairs of vertices into the set 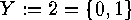 , where
we put
, where
we put
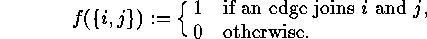
For example, the first one of the two labelled graphs of figure  can be identified in this way with the mapping
can be identified in this way with the mapping 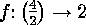 defined by
defined by
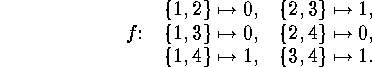
- The symmetric group
 acts
on
acts
on 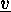 and hence also on
and hence also on
 , so that we obtain an action
of
, so that we obtain an action
of  on
on 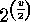 which is of the form
which is of the form 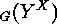 as
was described in
as
was described in  . Two labelled graphs are called
isomorphic
if and only if
they lie in the same orbit under this action, i.e. if and only if
each arises
from the other by renumbering the vertices, so that for example the
labelled graphs of figure
. Two labelled graphs are called
isomorphic
if and only if
they lie in the same orbit under this action, i.e. if and only if
each arises
from the other by renumbering the vertices, so that for example the
labelled graphs of figure  are isomorphic (apply
are isomorphic (apply
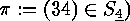 .
.
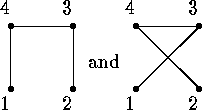
Figure: Two isomorphic labelled graphs with 4 vertices
- A graph
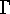 on
on  vertices is defined to be such an isomorphism
class of labelled graphs. It can be visualized by taking any member of the
isomorphism class and deleting the labels.This yields for the
labelled graphs shown in figure
vertices is defined to be such an isomorphism
class of labelled graphs. It can be visualized by taking any member of the
isomorphism class and deleting the labels.This yields for the
labelled graphs shown in figure  the
drawings of figure
the
drawings of figure  .
.
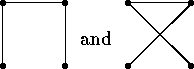
Figure: The graphs obtained from the labelled ones above
It should be clear by now what we
mean by a graph, and that in our terminology a graph is
not a pair 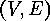 consisting of a set
consisting of a set  of vertices and a set
of vertices and a set 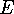 of
edges, but that a graph
of
edges, but that a graph 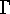 can be represented by such a pair,
so that, for example, the graphs of figure
can be represented by such a pair,
so that, for example, the graphs of figure  are in fact equal.
are in fact equal.
- If we want to allow multiple edges, say
up to the multiplicity
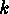 , then
we again consider
, then
we again consider 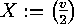 , but we change
, but we change 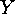 into
into
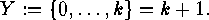 The elements of
The elements of

are called labelled 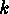 -graphs
, while by
-graphs
, while by 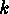 -graphs
on
-graphs
on  vertices
we mean the orbits of
vertices
we mean the orbits of  on this set.
on this set.
- If we want to allow loops or
multiple loops, we replace
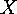 by the
union
by the
union 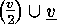 , and now
, and now 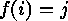 ,
for
,
for 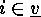 , means that
the vertex with the number
, means that
the vertex with the number  carries a
carries a 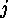 -fold loop.
-fold loop.
- If we want to consider digraphs
(i.e. the edges are directed and
neither loops nor parallel edges are allowed), we simply put

the set of injective pairs over  .
.

Thus graphs, 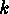 -graphs,
-graphs, 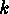 -graphs with loops
and also digraphs can be
considered as symmetry classes of mappings. Several other structures
will later on be obtained in the same way. Having defined the graphs
this way we want to count them by an application of
-graphs with loops
and also digraphs can be
considered as symmetry classes of mappings. Several other structures
will later on be obtained in the same way. Having defined the graphs
this way we want to count them by an application of  which
means that we have to derive a formula for
which
means that we have to derive a formula for 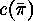 , the number of
cyclic factors of
, the number of
cyclic factors of 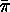 , the permutation induced by
, the permutation induced by 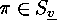 on the set
on the set  of pairs of points,
expressed in terms of the
cycle structure of
of pairs of points,
expressed in terms of the
cycle structure of  . In fact we can do better, we can derive the
cycle type of
. In fact we can do better, we can derive the
cycle type of 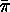 from the cycle type of
from the cycle type of  .
.




Next: The cycle type
Up: Actions
Previous: Enumeration of symmetry
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
 .
. Example
We would like to derive from
Example
We would like to derive from  vertices. Before we start doing so it should be mentioned
that this example is the second typical example which we present.
The first
examples
were devoted to the
introduction of group theoretical concepts,
to
the derivation of Sylow's Theorem
and to a
number theoretic result of Fermat.
The only example where a suitable choice of
vertices. Before we start doing so it should be mentioned
that this example is the second typical example which we present.
The first
examples
were devoted to the
introduction of group theoretical concepts,
to
the derivation of Sylow's Theorem
and to a
number theoretic result of Fermat.
The only example where a suitable choice of  and
and 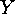 was made in order to define and enumerate a mathematical structure
was in fact
the composition of two symmetric groups.
As this example
may have been a little bit artificial we admit that it is
only now that we start to apply our paradigmatic actions more systematically.
Let us see how suitably chosen
was made in order to define and enumerate a mathematical structure
was in fact
the composition of two symmetric groups.
As this example
may have been a little bit artificial we admit that it is
only now that we start to apply our paradigmatic actions more systematically.
Let us see how suitably chosen  ,
, 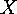 and
and 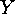 can be used in order to define
and enumerate the graphs on
can be used in order to define
and enumerate the graphs on  vertices.(Later on we shall refine this method
by counting these graphs according to the number of edges or according
to their automorphism group. Finally we shall even use this Ansatz
in order to construct such graphs and also to generate them
uniformly at random.) The way of defining
graphs as orbits of groups may at first glance seem to be circumstantial,
but we shall see that this definition is very flexible since it can easily be
generalized to all other kinds of graphs like multigraphs, directed graphs
and so on.
vertices.(Later on we shall refine this method
by counting these graphs according to the number of edges or according
to their automorphism group. Finally we shall even use this Ansatz
in order to construct such graphs and also to generate them
uniformly at random.) The way of defining
graphs as orbits of groups may at first glance seem to be circumstantial,
but we shall see that this definition is very flexible since it can easily be
generalized to all other kinds of graphs like multigraphs, directed graphs
and so on.
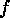 from the set
from the set
 of
(unordered) pairs of vertices into the set
of
(unordered) pairs of vertices into the set 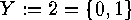 , where
we put
, where
we put
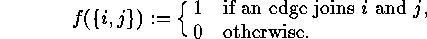
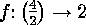 defined by
defined by
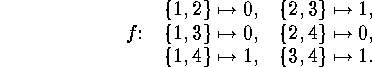
 acts
on
acts
on 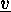 and hence also on
and hence also on
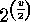 which is of the form
which is of the form 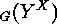 as
was described in
as
was described in 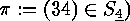 .
.
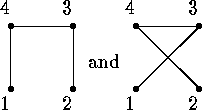
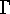 on
on 
 consisting of a set
consisting of a set  of vertices and a set
of vertices and a set  of
edges, but that a graph
of
edges, but that a graph 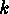 , then
we again consider
, then
we again consider 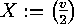 , but we change
, but we change 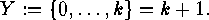 The elements of
The elements of

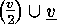 , and now
, and now 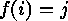 ,
for
,
for 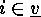 , means that
the vertex with the number
, means that
the vertex with the number  carries a
carries a 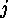 -fold loop.
-fold loop.

 .
.

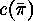 , the number of
cyclic factors of
, the number of
cyclic factors of 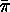 , the permutation induced by
, the permutation induced by 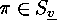 on the set
on the set  . In fact we can do better, we can derive the
cycle type of
. In fact we can do better, we can derive the
cycle type of