Enumeration of symmetry classes




Next: Graphs
Up: Actions
Previous: Examples
Our
paradigmatic examples
are the actions of  ,
,  ,
,  and
and 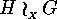 on
on 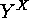 , obtained from given actions
, obtained from given actions  and
and 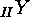 . The
orbits of these groups are called symmetry classes of mappings.
If
we want to be more explicit, we call them
. The
orbits of these groups are called symmetry classes of mappings.
If
we want to be more explicit, we call them  -classes,
-classes,
 -classes,
-classes,  -classes and
-classes and 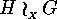 -classes, respectively. Their total number can be
obtained by an application of the Cauchy-Frobenius Lemma as soon as we know
the number of fixed points for each element of the respective group. In order
to derive these numbers we characterize the fixed points of each
-classes, respectively. Their total number can be
obtained by an application of the Cauchy-Frobenius Lemma as soon as we know
the number of fixed points for each element of the respective group. In order
to derive these numbers we characterize the fixed points of each 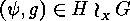 on
on 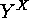 and then we use the natural embedding of
and then we use the natural embedding of
 ,
,  and
and  in
in 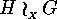 as described above.
Thus the following
lemma will turn out to be crucial:
as described above.
Thus the following
lemma will turn out to be crucial:
 .
. Lemma
Consider an
Lemma
Consider an 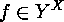 , an element
, an element
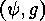 of
of 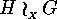 and assume that
and assume that
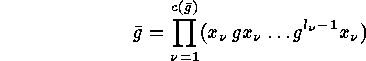
is the disjoint cycle decomposition of
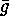 , the permutation of
, the permutation of 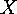 which corresponds to
which corresponds to 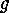 .
Then
.
Then 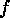 is a fixed point of
is a fixed point of 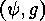 if and only if
the following two conditions
hold:
if and only if
the following two conditions
hold:
- Each
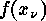 is a fixed point of the
cycleproduct
is a fixed point of the
cycleproduct 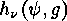 :
:

- The other values of
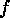 arise from the
values
arise from the
values 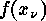 according to
the following equations:
according to
the following equations:
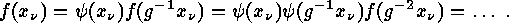
Proof:  says that
says that 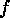 is fixed under
is fixed under 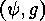 if and only if
its values
if and only if
its values 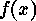 satisfy the equations
satisfy the equations
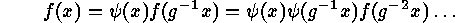

where 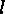 denotes the length of the cyclic factor of
denotes the length of the cyclic factor of 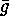 containing the point
containing the point 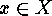 . Hence in particular the following must be
true:
. Hence in particular the following must be
true:
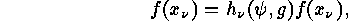
which means that 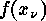 is a fixed point of
is a fixed point of 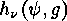 , as claimed.
Thus any fixed
, as claimed.
Thus any fixed 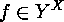 clearly has the stated properties, and vice
versa.
clearly has the stated properties, and vice
versa.

This, together with the Cauchy-Frobenius Lemma, yields the number of
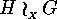 -classes on
-classes on 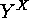 , and the restrictions to the subgroups
, and the restrictions to the subgroups  ,
,  and
and  give the numbers of
give the numbers of  -,
-,  - and
- and  -classes
on
-classes
on 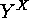 :
:
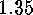 .
. Theorem
If both
Theorem
If both  and
and
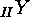 are finite actions, then we
obtain the following expression
for the total number of orbits of the corresponding action of
are finite actions, then we
obtain the following expression
for the total number of orbits of the corresponding action of
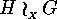 on
on 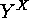 :
:

The restriction to  ,
,  and
and  according to
according to  yields:
yields:

and
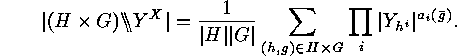
In order to apply these results to a
specific case it remains to evaluate
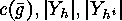 and
and 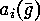 or
or 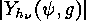 which still can be quite cumbersome as the following example
shows.
which still can be quite cumbersome as the following example
shows.
Try to
compute the number of symmetry classes of mappings
for various group actions. Furthermore you can compute a
transversal of G-classes
on 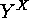 .
.




Next: Graphs
Up: Actions
Previous: Examples
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
 .
. Lemma
Consider an
Lemma
Consider an 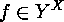 , an element
, an element
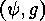 of
of 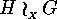 and assume that
and assume that
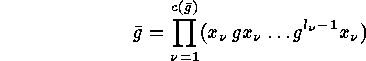
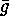 , the permutation of
, the permutation of 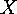 which corresponds to
which corresponds to 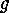 .
Then
.
Then 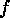 is a fixed point of
is a fixed point of 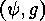 if and only if
the following two conditions
hold:
if and only if
the following two conditions
hold:
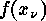 is a fixed point of the
cycleproduct
is a fixed point of the
cycleproduct 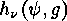 :
:

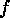 arise from the
values
arise from the
values 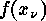 according to
the following equations:
according to
the following equations:
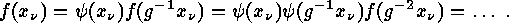
 ,
,  ,
,  and
and 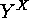 , obtained from given actions
, obtained from given actions  and
and 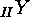 . The
orbits of these groups are called symmetry classes of mappings.
If
we want to be more explicit, we call them
. The
orbits of these groups are called symmetry classes of mappings.
If
we want to be more explicit, we call them 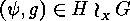 on
on 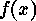 satisfy the equations
satisfy the equations
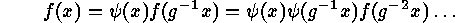

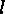 denotes the length of the cyclic factor of
denotes the length of the cyclic factor of 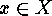 . Hence in particular the following must be
true:
. Hence in particular the following must be
true:
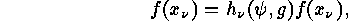

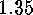 .
. Theorem
Theorem 

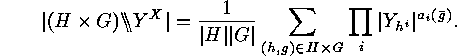
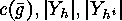 and
and 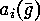 or
or 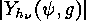 which still can be quite cumbersome as the following example
shows.
which still can be quite cumbersome as the following example
shows.