
 and
and 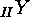 which form our paradigmatic examples, and which will be discussed in
full detail in later sections. In order to prepare this we form the set
of all the mappings from
which form our paradigmatic examples, and which will be discussed in
full detail in later sections. In order to prepare this we form the set
of all the mappings from 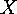 into
into 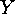 :
:

and notice:
If  acts on
acts on 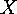 and
and  acts on
acts on 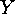 , then
, then
 ,
,  and
and  act on
act on 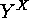 as follows:
as follows:
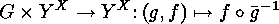 ,
i.e.
,
i.e. 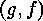 is
mapped onto
is
mapped onto 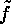 , where
, where 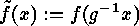 . The
corresponding permutation group on
. The
corresponding permutation group on 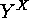 will be denoted by
will be denoted by 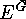 .
.
 i.e.
i.e. 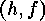 is
mapped onto
is
mapped onto 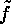 , where
, where 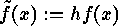 . The corresponding
permutation group will be denoted by
. The corresponding
permutation group will be denoted by 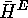 .
.
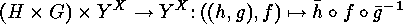 , i.e.
, i.e. 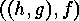 is mapped onto
is mapped onto 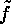 , where
, where
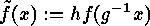 . The corresponding permutation
group on
. The corresponding permutation
group on 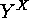 will be denoted by
will be denoted by 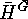 , and it
will be called the power group of
, and it
will be called the power group of 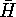 by
by  .
.
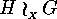 : Its underlying set is
: Its underlying set is

and the multiplication is defined by
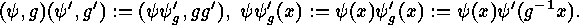
The actions  and
and  yield the following natural
action of
yield the following natural
action of  on
on  :
:
The corresponding permutation group
on 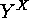 will be denoted by
will be denoted by 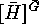 , and it will be
called the exponentiation group
of
, and it will be
called the exponentiation group
of 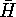 by
by  . The orbits of
. The orbits of 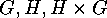 and
and 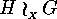 on
on
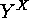 will be called symmetry classes of mappings
of mappings.
will be called symmetry classes of mappings
of mappings.
A few remarks concerning the wreath
product 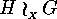 are in order, they
will in particular show that the actions of
are in order, they
will in particular show that the actions of  ,
,  , and
, and  on
on
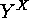 are restrictions
of the action of
are restrictions
of the action of 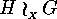 on
on 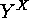 defined above. The reader is kindly asked
carefully to check the following statements on wreath products
defined above. The reader is kindly asked
carefully to check the following statements on wreath products 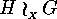 :
:
 .
. Lemma
The wreath product
Lemma
The wreath product 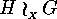 has the following
properties:
has the following
properties:
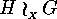 is
is  , where
, where 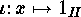 .
.
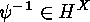 by
by 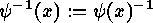 , we get
, we get
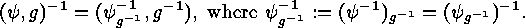
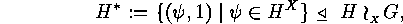
is called the base group, and it is the direct product of
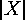 copies
copies 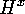 of
of  :
:
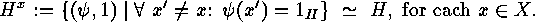
 is a complement of
is a complement of  , so that we have
, so that we have
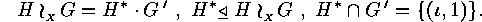
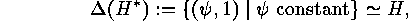
satisfies
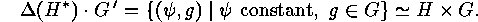
 ,
, 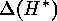 and
and
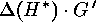 are natural embeddings of
are natural embeddings of  ,
,  and
and  into
into 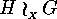 , in short:
, in short:
so that in fact the actions of  ,
,  , and
, and  on
on 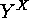 introduced above are restrictions of the
action of
introduced above are restrictions of the
action of 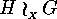 on
on 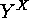 .
.
In order to prepare later applications of such actions we mention
that actions of direct products and of wreath products can be
reformulated in terms of the respective factors of the direct and of the
wreath product. Here is, to begin with, a lemma on actions of direct products,
which is very easy to check (exercise ![]() ):
):
Exercises
E 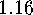 .
. Show that
Show that 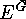 is normal in
is normal in 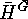 and in
and in 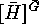 , and that
, and that 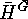 is not in general normal in
is not in general normal in
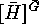 . Check that the factor group
. Check that the factor group 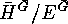 is isomorphic to
is isomorphic to 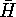 , while
, while 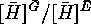 is isomorphic to
is isomorphic to  . What does
this mean,
in the light of exercise
. What does
this mean,
in the light of exercise ![]() , for the enumeration of the orbits of
, for the enumeration of the orbits of
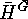 and
and 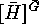 ?
?