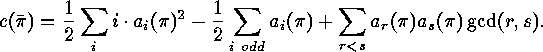The cycle type of the induced action on 2-subsets




Next: Enumeration of Graphs
Up: Actions
Previous: Graphs
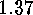 .
. Lemma
If
Lemma
If 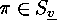 , then
, then
- Each
 -cycle of
-cycle of  ,
,  odd, contributes to
odd, contributes to 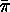 exactly
exactly
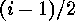 cyclic factors, each of which is an
cyclic factors, each of which is an  -cycle.
-cycle.
- Each
 -cycle of
-cycle of  ,
,  even,
contributes to
even,
contributes to 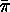 exactly one
cycle of length
exactly one
cycle of length 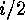 and
and 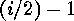 further cycles, which are of length
further cycles, which are of length  .
.
- Each pair of cyclic factors of
 , say
an
, say
an  -cycle and a
-cycle and a 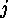 -cycle,
contributes to
-cycle,
contributes to 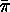 exactly
exactly 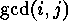 cyclic factors, each of which
has the length
cyclic factors, each of which
has the length 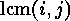 .
.
- All the cyclic factors of
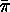 arise in this way.
arise in this way.
Proof:
i) First let  be odd. Without loss of generality we may
assume that the
be odd. Without loss of generality we may
assume that the  -cycle in question is
-cycle in question is
 . Consider a positive
. Consider a positive  . Then
. Then
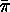 contains the following cyclic permutation of
contains the following cyclic permutation of  -subsets:
-subsets:
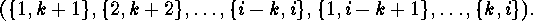
This cycle is of length  , and the cycles of this form arising from
different
, and the cycles of this form arising from
different  are pairwise disjoint. Furthermore these are all
the cycles arising from
are pairwise disjoint. Furthermore these are all
the cycles arising from  since, for each such
since, for each such 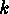 , we have,
as
, we have,
as  is odd:
is odd:
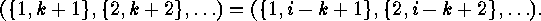
ii) If  is even, say
is even, say  , we
may assume that the cyclic factor of
, we
may assume that the cyclic factor of
 is
is 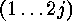 . It yields, for
. It yields, for 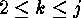 , the
, the 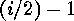 different
different
 -cycles
-cycles
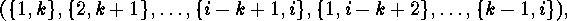
together with the  -cycle
-cycle

iii) A pair of cyclic factors of  , say
the pair
, say
the pair  contributes to
contributes to  the following product of disjoint cycles:
the following product of disjoint cycles:
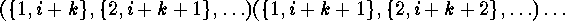
The length of each of these cyclic factors is 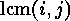 , and their number
is therefore equal to
, and their number
is therefore equal to 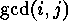 .
.
iv) is clear.

This lemma yields the cycle structure
of 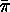 and the desired
number
and the desired
number 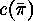 of cyclic factors which we need in order to evaluate
the number of graphs on
of cyclic factors which we need in order to evaluate
the number of graphs on  vertices by an application of the Cauchy-Frobenius
Lemma:
vertices by an application of the Cauchy-Frobenius
Lemma:
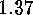 .
. Corollary
For each
Corollary
For each 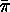 on
on  we have:
we have:
- If
 is odd, then
is odd, then

- If
 is even, then
is even, then

- The total number of cyclic factors is
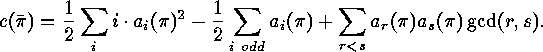
In the next two programs you can enter a permutation and compute the
cycle type
and the
total number of cyclic factors
of the induced permutation on  -subsets.
-subsets.




Next: Enumeration of Graphs
Up: Actions
Previous: Graphs
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
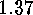 .
. Lemma
If
Lemma
If 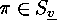 , then
, then
 -cycle of
-cycle of  ,
,  odd, contributes to
odd, contributes to 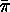 exactly
exactly
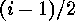 cyclic factors, each of which is an
cyclic factors, each of which is an  -cycle.
-cycle.
 -cycle of
-cycle of  ,
,  even,
contributes to
even,
contributes to 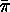 exactly one
cycle of length
exactly one
cycle of length 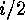 and
and 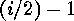 further cycles, which are of length
further cycles, which are of length  .
.
 , say
an
, say
an  -cycle and a
-cycle and a 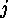 -cycle,
contributes to
-cycle,
contributes to 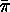 exactly
exactly 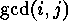 cyclic factors, each of which
has the length
cyclic factors, each of which
has the length 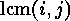 .
.
 arise in this way.
arise in this way.
 . Consider a positive
. Consider a positive  . Then
. Then
 -subsets:
-subsets:
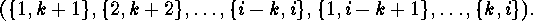
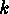 , we have,
as
, we have,
as 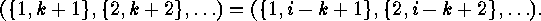
 , we
may assume that the cyclic factor of
, we
may assume that the cyclic factor of
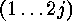 . It yields, for
. It yields, for 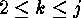 , the
, the 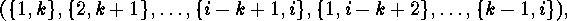
 -cycle
-cycle

 contributes to
contributes to 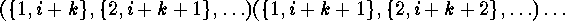

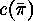 of cyclic factors which we need in order to evaluate
the number of graphs on
of cyclic factors which we need in order to evaluate
the number of graphs on  vertices by an application of the Cauchy-Frobenius
Lemma:
vertices by an application of the Cauchy-Frobenius
Lemma:
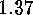 .
.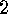 Corollary
Corollary  we have:
we have: