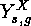 is the set
of surjective mappings
is the set
of surjective mappings 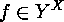 which are constant on the
which are constant on the  cyclic factors of
cyclic factors of 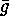 . Hence this set can be identified with
the set
. Hence this set can be identified with
the set 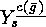 .
More generally we consider the set
.
More generally we consider the set
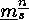 and define the numbers
and define the numbers
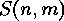 by
by
These considerations lead to various combinatorial numbers
so that a few
remarks concerning these are in order. For example, 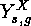 is the set
of surjective mappings
is the set
of surjective mappings 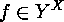 which are constant on the
which are constant on the  cyclic factors of
cyclic factors of 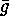 . Hence this set can be identified with
the set
. Hence this set can be identified with
the set 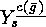 .
More generally we consider the set
.
More generally we consider the set
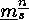 and define the numbers
and define the numbers
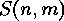 by
by
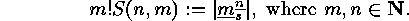
These 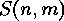 are called the Stirling numbers
of the second
kind . If
are called the Stirling numbers
of the second
kind . If 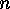 is used as row index and
is used as row index and  as column index, then the upper
left hand corner of the table of Stirling numbers of the second kind is as
follows:
as column index, then the upper
left hand corner of the table of Stirling numbers of the second kind is as
follows:
There is a program for computing the stirling second numbers.
By definition
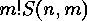 is equal
to the number of ordered set partitions
is equal
to the number of ordered set partitions
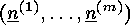 of
of 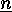 into
into  blocks,
i.e. into
blocks,
i.e. into  nonempty subsets
nonempty subsets 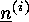 .
This is clear since each such ordered partition
can be identified with
.
This is clear since each such ordered partition
can be identified with 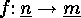 where
where 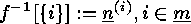 . Thus
. Thus
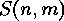 is the number of set partitions
is the number of set partitions
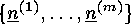 of the set
of the set 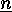 into
into  blocks, and
hence
blocks, and
hence 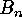 , the number of all the set partitions of
, the number of all the set partitions of 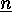 satisfies
the equation
satisfies
the equation
These numbers 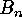 are called Bell numbers .
There is a program for
computing the Bell numbers.
are called Bell numbers .
There is a program for
computing the Bell numbers.
Another consequence
of the definition of Stirling numbers of the second kind and ![]() is
is
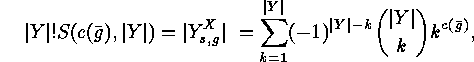
which implies:
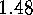 .
. Stirling's Formula
For
Stirling's Formula
For  and any natural number
and any natural number 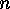 we have:
we have:
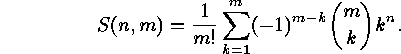
Another series of combinatorial numbers shows up if we rewrite ![]() in
the following form:
in
the following form:
We put
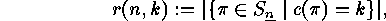
and call these the signless
Stirling numbers of the first kind.
They satisfy the following recursion formula, since in 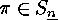 the point
the point 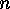 either forms a 1-cycle or does not:
either forms a 1-cycle or does not:
while the initial values are 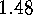 .
.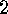 Lemma For
Lemma For 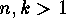 we have
we have

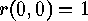 and
and 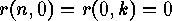 , for
, for 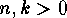 .
.
The upper left hand corner of a table containing
these numbers 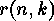 , for
, for
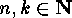 , is as follows
, is as follows
There is a program for computing the stirling first numbers.
We now return to the number 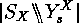 . The exercise
. The exercise ![]() together with the identity
together with the identity ![]() yields
yields
Another series of combinatorial numbers arises when we count certain injective
symmetry classes,
since ![]() implies
implies
where  .
It is easy to derive these numbers from the rencontre numbers
.
It is easy to derive these numbers from the rencontre numbers
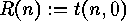 , since obviously the following is true:
, since obviously the following is true:
This can be made more explicit by an application of exercise
![]() which yields
which yields
There is a program for computing the recontre numbers and their generalization.
Now we use that, for 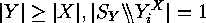 , so that by the last three equations:
, so that by the last three equations:
It is in fact an important and interesting task of enumeration theory to derive identities in this way since they are understood as soon as they are seen to describe a combinatorial situation. Another example is the identity
 .
. Lemma For natural numbers
Lemma For natural numbers 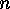 and
and 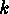 the following
identities hold:
the following
identities hold:
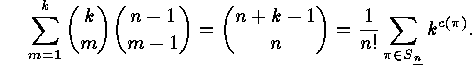
Proof: Exercise ![]() implies
that, for
implies
that, for  ,
,

is equal to the number of symmetry classes of 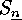 on
on
 , the elements of which satisfy
, the elements of which satisfy
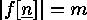 . Thus
the left hand side is
. Thus
the left hand side is 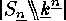 . But
the orbit of
. But
the orbit of  under
under 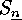 is characterized by the orders
of the inverse images
is characterized by the orders
of the inverse images 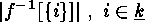 . Hence the
number of these orbits is equal to the number of
. Hence the
number of these orbits is equal to the number of 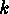 -tupels
-tupels 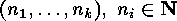 , and
, and 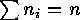 , therefore
the first identity follows from
exercise
, therefore
the first identity follows from
exercise ![]() . The last
equation is already clear
from
. The last
equation is already clear
from ![]() .
.

Exercises
E 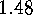 .
. Use the Principle of Inclusion and Exclusion in order to prove
Use the Principle of Inclusion and Exclusion in order to prove ![]() .
.
E 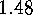 .
. Show that the number of
Show that the number of 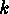 -tupels
-tupels 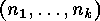 such that
such that
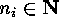 and
and 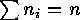 is equal to
is equal to

E  .
. Prove that the Stirling numbers of the second kind satisfy the equation
Prove that the Stirling numbers of the second kind satisfy the equation
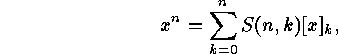
where 