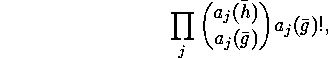
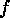 is injective if and only if the mapping described
in the first item of
is injective if and only if the mapping described
in the first item of 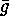 and
and
 have the same length. The number of such mappings is
have the same length. The number of such mappings is
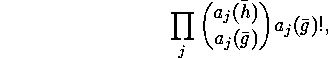
while the second item of ![]() says that we have to multiply this number by
says that we have to multiply this number by  in order to get the number
in order to get the number 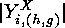 of fixed points of
of fixed points of 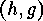 on
on 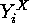 . Thus we have proved
. Thus we have proved
and hence, by
restriction, the numbers of fixed points of
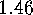 .
.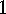 Corollary The number of fixed points of
Corollary The number of fixed points of 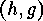 on
on
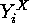 is
is
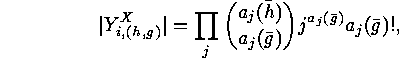
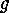 and of
and of 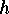 are:
are:
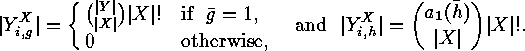
An application of the Cauchy-Frobenius Lemma yields the desired number of injective symmetry classes:
so that we obtain by restriction the number of injective
and the number of injective
 .
.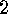 Theorem The number of injective
Theorem The number of injective
 -classes is
-classes is
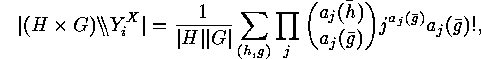
 -classes
-classes
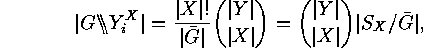
 -classes
-classes


Try to compute the number of injective symmetry classes for various group actions.
Exercises
E  .
.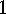
 is called
is called 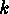 - fold transitive
if and only if
the corresponding action of
- fold transitive
if and only if
the corresponding action of  on the set of
on the set of 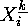 of injective mapping is
transitive:
of injective mapping is
transitive:

Prove that, in case of a transitive action  , this is equivalent to:
, this is equivalent to:
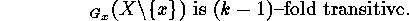
E 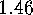 .
.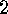 Prove that
Prove that  is divisible by
is divisible by 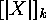 if
if  is finite
and
is finite
and 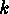 -fold transitive.
-fold transitive.
E 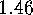 .
.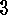 Show that
Show that 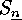 is
is 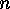 -fold transitive on
-fold transitive on
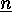 while
while 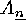 is
is 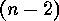 -fold transitive on
-fold transitive on 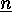 , but not
, but not  -fold
transitive, for
-fold
transitive, for 