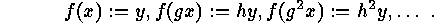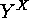 and consider its subsets consisting of the injective
and the surjective maps
and consider its subsets consisting of the injective
and the surjective maps 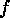 only:
only:
We now return to 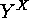 and consider its subsets consisting of the injective
and the surjective maps
and consider its subsets consisting of the injective
and the surjective maps 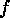 only:
only:
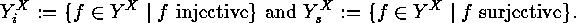
It is clear
that each of these sets is both a  -set and an
-set and an  -set and therefore it
is also an
-set and therefore it
is also an  -set, but it will not in general
be an
-set, but it will not in general
be an 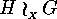 -set.
The corresponding orbits of
-set.
The corresponding orbits of 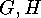 and
and  on
on 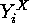 are called
injective
symmetry classes, while those on
are called
injective
symmetry classes, while those on  will be called
surjective
symmetry classes. We should like to determine their number.
In order to do this we describe the fixed points
of
will be called
surjective
symmetry classes. We should like to determine their number.
In order to do this we describe the fixed points
of 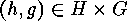 on these sets to prepare an application of the
Cauchy-Frobenius Lemma. A first remark shows how the fixed points of
on these sets to prepare an application of the
Cauchy-Frobenius Lemma. A first remark shows how the fixed points of 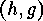 on
on 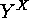 can be constructed with the aid of
can be constructed with the aid of  and
and 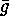 ,
the permutations induced by
,
the permutations induced by 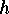 on
on 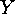 and by
and by 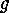 on
on 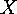 (use
(use ![]() ):
):
and
the other values of
 .
.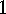 Corollary If
Corollary If  , then
, then 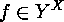 is fixed under
is fixed under 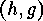 if and only if
the following two conditions
are satisfied:
if and only if
the following two conditions
are satisfied:

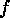 arise from
the values
arise from
the values 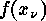 according to
according to

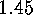 .
. Corollary The fixed points of
Corollary The fixed points of 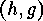 are
the
are
the 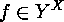 which can be
obtained in the following way:
which can be
obtained in the following way:
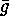 , let
, let 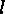 denote its length, we
associate a cyclic factor of
denote its length, we
associate a cyclic factor of
 of length
of length 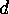 dividing
dividing 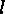 .
.
 is a point in this cyclic factor
of
is a point in this cyclic factor
of 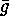 and
and 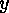 a point
in the chosen cyclic factor of
a point
in the chosen cyclic factor of  , then put
, then put