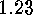 .
.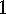 Lemma
For each natural number
Lemma
For each natural number  the power
the power 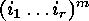 consists
of exactly
consists
of exactly
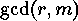 disjoint cyclic factors, they all are
of length
disjoint cyclic factors, they all are
of length 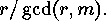
Another useful result describes the cycle structure of a power of a cycle:
 .
. Lemma
For each natural number
Lemma
For each natural number  the power
the power 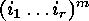 consists
of exactly
consists
of exactly
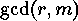 disjoint cyclic factors, they all are
of length
disjoint cyclic factors, they all are
of length 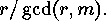
Proof: Let 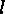 denote the length of the cyclic
factor of
denote the length of the cyclic
factor of 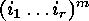 containing
containing 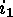 . This cycle is
. This cycle is
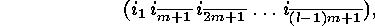
where 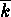 denotes the residue class of
denotes the residue class of 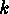 modulo
modulo  .
Correspondingly the cyclic factor containing
.
Correspondingly the cyclic factor containing 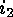 (if
(if 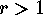 ) must be
) must be
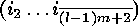 , so that all the cyclic factors of
, so that all the cyclic factors of
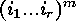 have the same length
have the same length 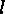 . Thus
. Thus 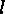 is
the order of
is
the order of 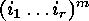 , an element of the group
, an element of the group
 which is of order
which is of order  . Hence
. Hence  divides
divides
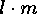 and
and 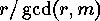 divides
divides 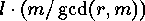 and
therefore also
and
therefore also 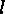 .
But
.
But
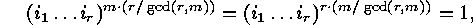
so that also 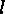 must divide
must divide 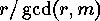 , which proves that
in fact
, which proves that
in fact 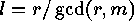 .
.

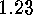 .
. Corollary
The elements of order
Corollary
The elements of order 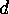 in the group generated
by the cycle
in the group generated
by the cycle  are the powers
are the powers 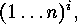 where
where  is
of the form
is
of the form 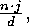 and
and  is relatively prime to
is relatively prime to 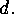
A direct consequence of this is
These 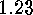 .
. Corollary
The group
Corollary
The group 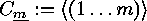 contains, for each divisor
contains, for each divisor 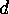 of
of  exactly one subgroup
exactly one subgroup 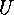 of
order
of
order 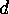 . Furthermore, this subgroup contains
. Furthermore, this subgroup contains 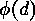 elements
consisting of
elements
consisting of 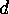 -cycles only,
if
-cycles only,
if 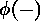 denotes
the Euler function
denotes
the Euler function 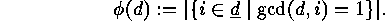
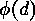 elements form the set of generators of
elements form the set of generators of 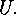
As finite cyclic groups of the same order are isomorphic, they have the same properties:
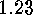 .
.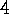 Corollary
A finite cyclic group
Corollary
A finite cyclic group  has,
for each divisor
has,
for each divisor 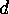 of its order
of its order  exactly one subgroup
exactly one subgroup 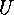 of
order
of
order 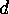 . Furthermore, this subgroup contains
. Furthermore, this subgroup contains 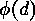 generators, and
so,
generators, and
so,  has exactly
has exactly 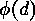 elements of this particular order. Moreover
elements of this particular order. Moreover

Exercises
E  .
.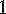 Show that, for each
Show that, for each 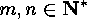 and
and 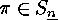 , the permutations
, the permutations
 and
and  are conjugate, if and
only if
are conjugate, if and
only if  and each length of a cyclic factor of
and each length of a cyclic factor of  are relatively prime.
are relatively prime.
E  .
.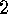 Prove that the invertibility of the matrix
Prove that the invertibility of the matrix

is equivalent to the following fact:
Two elements 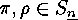 are equivalent if and only if,
for each
are equivalent if and only if,
for each 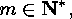 the number of cyclic factors of
the number of cyclic factors of  and of
and of  are equal:
are equal:

(Later on we shall return to this and give a proof of the regularity of
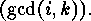 We shall in fact show that the determinant of this
matrix is
We shall in fact show that the determinant of this
matrix is 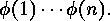 )
)