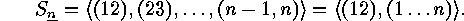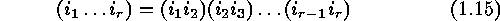
Since
each cycle, and hence every element of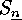 
, can be written as a product
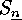of transpositions. Thus is generated by its subset of transpositions
(if this is empty, then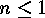 
, and both 
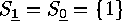are generated by the empty set
). But, except for the case when 
, we do not need every
transposition in order to generate the symmetric group, since, for
, we derive from 
that
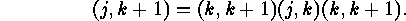
Thus the transposition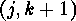 
can be obtained from 
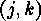by
conjugation with the transposition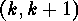 
of adjacent points. Therefore
the subset
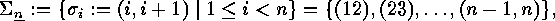
consisting of the elementary transpositions
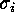, generates
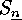. A further system of generators of 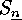is obtained from
so that we have proved
.
Corollary