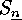 is in fact a Coxeter group,
which means that
there exists a set of generators
is in fact a Coxeter group,
which means that
there exists a set of generators 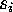 such that the relations
are of the particular form
such that the relations
are of the particular form  where
where
Reduced decompositions play a role also in the theory of other groups.
The symmetric group 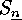 is in fact a Coxeter group,
which means that
there exists a set of generators
is in fact a Coxeter group,
which means that
there exists a set of generators 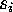 such that the relations
are of the particular form
such that the relations
are of the particular form  where
where
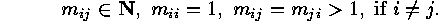
In the case of the symmetric group 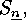 the Coxeter system of generators is the
subset
the Coxeter system of generators is the
subset
 of elementary transpositions
of elementary transpositions  as we have
seen already.
Furthermore, this leads us to introduce the weak
Bruhat order
as we have
seen already.
Furthermore, this leads us to introduce the weak
Bruhat order
 on
on 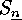 , which is the transitive closure of
, which is the transitive closure of

The Bruhat order of the symmetric group 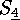 is shown in figure
is shown in figure ![]() .
We note that the number of reduced decompositions (and also the set of reduced decompositions)
can be obtained by going from the identity upwards in all the possible ways until the permutation in
question is reached.
.
We note that the number of reduced decompositions (and also the set of reduced decompositions)
can be obtained by going from the identity upwards in all the possible ways until the permutation in
question is reached.
We are now approaching a famous result on reduced sequences for the proof of
which we need a better knowledge of the set of inversions.
In order to describe how 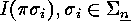 , arises from
, arises from
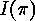 , we use that
, we use that 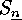 acts on
acts on 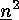 in a canonic way:
in a canonic way: 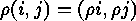 . Keeping this in mind, we easily obtain:
. Keeping this in mind, we easily obtain:
This yields for the corresponding reduced lengths:
in accordance with ![]() .
If
.
If 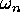 denotes the permutation
denotes the permutation 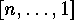 of maximal length,
then
of maximal length,
then
Proof: Clearly 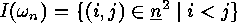 , and hence
, and hence
 . Moreover
. Moreover

so 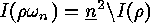 , and
, and
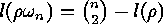 . Finally we note that
. Finally we note that
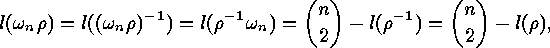
which completes the proof.

An expression
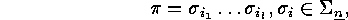
of  in terms of elementary transpositions and minimal
in terms of elementary transpositions and minimal
 was called a reduced decomposition
of
was called a reduced decomposition
of  . The set of corresponding
sequences of indices is indicated as follows:
. The set of corresponding
sequences of indices is indicated as follows:

These sequences are called reduced sequences
of  .
.