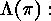
The Lehmer code
is the sequence of numbers of white buttons in the columns of 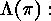
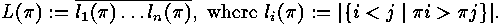
For example
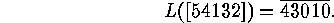
If it is clear which 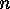 is meant, then we may replace
is meant, then we may replace 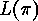 by the
shorter sequence
by the
shorter sequence

arising from 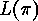 by canceling the zeros at the end of
by canceling the zeros at the end of 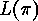 , for
example
, for
example
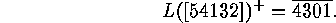
It is not difficult to see
how 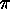 can be reconstructed from
can be reconstructed from 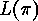 . Clearly
. Clearly 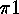 is the
is the 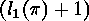 -th element of
-th element of 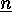 , with respect to the natural order of
, with respect to the natural order of 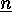 .
Correspondingly,
.
Correspondingly, 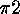 is the
is the 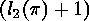 -th element of
-th element of
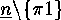 , and so on. For example
, and so on. For example
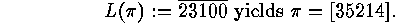
Furthermore, each 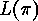 ,
, 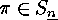 , is
, is 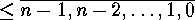 , i.e.
, i.e.
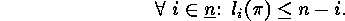
Since there are 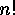 such
sequences in
such
sequences in 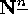 , we have obtained:
, we have obtained:
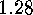 .
. Corollary
The Lehmer code establishes a bijection
between
Corollary
The Lehmer code establishes a bijection
between 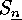 and the set of sequences
and the set of sequences  in
in 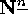 ,
, 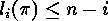 , for each
, for each 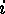 .
.
This shows that in fact the Lehmer code is a code for permutations.
But there is much more to say about Lehmer codes. Applying the equivalences
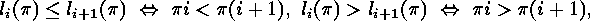
we can easily derive (exercise ![]() )
that right multiplication of
)
that right multiplication of 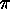 by the elementary
transposition
by the elementary
transposition 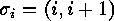 has the following effect on
has the following effect on 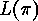 :
:
if
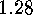 .
.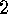 Lemma
For each
Lemma
For each 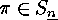 and each
and each 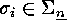 we have
we have
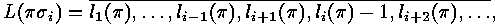
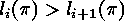 , while
, while
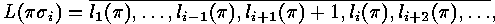
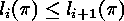 .
.
The main point is that the shift from 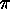 to
to 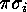 amounts
(cf.
amounts
(cf. ![]() ) to an increase or a decrease in
) to an increase or a decrease in

by 1. Hence the following holds:
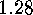 .
.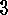 Corollary
The sum
Corollary
The sum 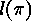 of the entries of the
Lehmer code
of the entries of the
Lehmer code 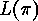 of
of 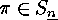 is equal to the minimal number of
elementary transpositions
is equal to the minimal number of
elementary transpositions 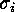 which are needed in order to express
which are needed in order to express
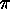 as a product of elementary transpositions. Moreover, this yields a
canonic way of expressing
as a product of elementary transpositions. Moreover, this yields a
canonic way of expressing 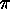 as a product of
as a product of 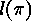 elementary
transpositions by decreasing the rightmost nonzero entry of the Lehmer code
by 1 and iterating this process until each entry is equal to zero.
elementary
transpositions by decreasing the rightmost nonzero entry of the Lehmer code
by 1 and iterating this process until each entry is equal to zero.
We therefore call 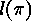 the
reduced length
of
the
reduced length
of 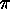 and we call such an expression of
and we call such an expression of 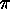 as a product of
as a product of
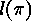 elementary transpositions, which is of minimal length, a
reduced decomposition.
A reduced decomposition of
elementary transpositions, which is of minimal length, a
reduced decomposition.
A reduced decomposition of 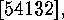 for example, is obtained from the following sequence of manipulations
of Lehmer codes, according to
for example, is obtained from the following sequence of manipulations
of Lehmer codes, according to
![]() :
:
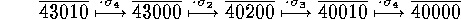
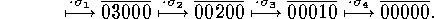
This shows that
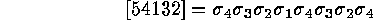
is a reduced decomposition. Try to compute the reduced composition of some permutations.
The lemma ![]() also shows how we can obtain all the
reduced decompositions of a given permutation:
also shows how we can obtain all the
reduced decompositions of a given permutation:
 .
. Corollary
The complete set of reduced decompositions of
Corollary
The complete set of reduced decompositions of 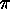 is obtained by carrying out all the successive
multiplications that reduce the Lehmer sequence by 1, according to
is obtained by carrying out all the successive
multiplications that reduce the Lehmer sequence by 1, according to ![]() .
.
Exercises