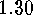 .
.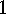 Lemma
If
Lemma
If 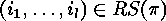 , then
, then
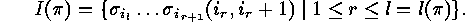
Proof: By induction on  . The case
. The case 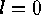 yields the empty set
which is in fact the set of inversions of
yields the empty set
which is in fact the set of inversions of  . If
. If 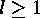 , then we
can consider
, then we
can consider 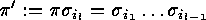 , which is of reduced length
, which is of reduced length 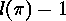 . The induction hypothesis gives
. The induction hypothesis gives
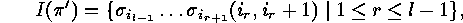
and from ![]() we know how
we know how 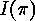 can be obtained from
can be obtained from 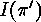 ,
since
,
since 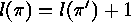 shows which of the two cases holds:
shows which of the two cases holds:
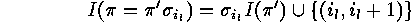

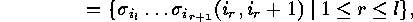
as it is stated.

We are now in a position to prove the following important result:
where 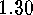 .
. The Exchange Lemma
If
The Exchange Lemma
If 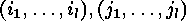 are elements of
are elements of 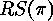 , then there exist
, then there exist
 such that
such that

 means that
means that  is left out.
is left out.
Proof: We know that
 and hence there exists an
and hence there exists an  such that
such that
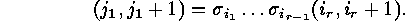
But this implies (since  transposes
transposes 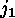 and
and 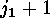 ):
):
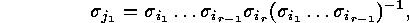
and so
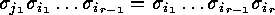 ,
which proves the statement.
,
which proves the statement.

This result will be used much later in order to introduce an important class
of polynomials, the Schubert polynomials. They correspond to the
permutations and form an
important basis of the polynomial ring 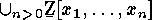 . They will be
defined with the aid of a differential operator that corresponds to a
reduced decomposition, and the Exchange Lemma will be used in order to
prove that this operator is independent of the chosen reduced decomposition.
Moreover, they form a natural generalization of the so-called Schur
polynomials which are important both for the enumeration theory of symmetry
classes of mappings and for the representation theory of symmetric groups.
. They will be
defined with the aid of a differential operator that corresponds to a
reduced decomposition, and the Exchange Lemma will be used in order to
prove that this operator is independent of the chosen reduced decomposition.
Moreover, they form a natural generalization of the so-called Schur
polynomials which are important both for the enumeration theory of symmetry
classes of mappings and for the representation theory of symmetric groups.