Isometry classes of linear codes



Next: Indecomposability
Up: Isometry Classes of Indecomposable
Previous: Notation
A linear 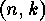 -code over the Galois field
-code over the Galois field 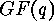 is a
is a
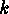 -dimensional subspace of the vector space
-dimensional subspace of the vector space  . As usual
codewords will be written as rows
. As usual
codewords will be written as rows  . A
. A 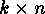 -matrix
-matrix 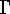 over
over 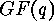 is called a generator matrix of the
linear
is called a generator matrix of the
linear 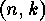 -code
-code 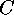 , if and only if the rows of
, if and only if the rows of 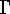 form a basis of
form a basis of
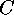 , so that
, so that 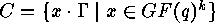 . Two linear
. Two linear
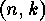 -codes
-codes 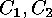 are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps
are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps  onto
onto
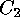 . Using the notion of finite group actions one can easily express
equivalence of codes in terms of the wreath product action introduced above:
. Using the notion of finite group actions one can easily express
equivalence of codes in terms of the wreath product action introduced above:
 and
and 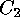 are equivalent, if and only if there exist
are equivalent, if and only if there exist  (where
(where 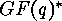 denotes the multiplicative group of the
Galois field) such that
denotes the multiplicative group of the
Galois field) such that  .
.
The complete monomial group 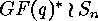 of degree
of degree  over
over
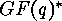 acts on
acts on  as it was described above (see
equation (2)) in the more general case of
as it was described above (see
equation (2)) in the more general case of  on
on 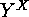 :
:
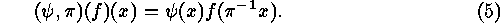
In order to apply the results of the theory of finite group actions, this
equivalence relation for linear 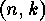 -codes is translated into an
equivalence relation for generator matrices of linear codes, and these
generator matrices are considered to be functions
-codes is translated into an
equivalence relation for generator matrices of linear codes, and these
generator matrices are considered to be functions 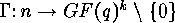 where
where 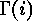 is the
is the 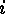 -th column of the
generator matrix
-th column of the
generator matrix 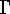 . (We exclude
. (We exclude  -columns for obvious reasons.)
-columns for obvious reasons.)
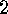 .
.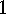 Theorem
The matrices corresponding to the two functions
Theorem
The matrices corresponding to the two functions 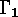 and
and 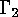 from
from  to
to 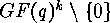 are generator matrices of two equivalent
codes, if and only if
are generator matrices of two equivalent
codes, if and only if 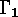 and
and 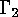 lie in the same orbit of the
following action of
lie in the same orbit of the
following action of 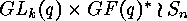 as permutation group on
as permutation group on
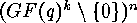 :
: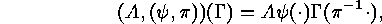
or, more explicitly,
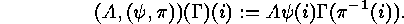
Following SLEPIAN, we use the following notation:
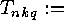
- the number of orbits of functions
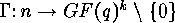 under the group action of 2.1, i.e.
under the group action of 2.1, i.e.
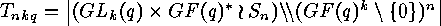 .
.
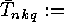
- the number of orbits of functions
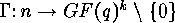 under the group action of 2.1, such that
for all
under the group action of 2.1, such that
for all 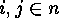 ,
, 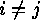 and all
and all  the value of
the value of
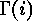 is different from
is different from 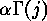 . (In the case
. (In the case 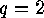 , this is
the number of injective functions
, this is
the number of injective functions 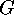 .)
.)
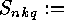
- the number of equivalence classes of linear
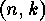 -codes
over
-codes
over 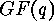 with no columns of zeros. (A linear
with no columns of zeros. (A linear 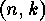 -code has columns of
zeros, if and only if there is some
-code has columns of
zeros, if and only if there is some 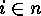 such that
such that 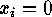 for all
codewords
for all
codewords  , and so we should exclude such columns.)
, and so we should exclude such columns.)
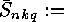
- the number of classes of injective linear
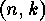 -codes over
-codes over 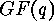 with no columns of zeros. (A linear
with no columns of zeros. (A linear 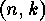 -code
is called injective, if and only if for all
-code
is called injective, if and only if for all 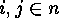 ,
, 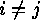 and
and  there is some codeword
there is some codeword  such that
such that 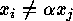 .)
.)
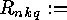
- the number of classes of indecomposable linear
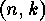 -codes over
-codes over 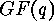 with no columns of zeros. (The definition of an
indecomposable code will be given later.)
with no columns of zeros. (The definition of an
indecomposable code will be given later.)

- the number of classes of indecomposable, injective
linear
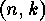 -codes over
-codes over 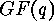 with no columns of zeros.
with no columns of zeros.
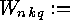
- be the number of classes of linear
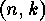 -codes over
-codes over
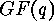 with columns of zeros allowed.
with columns of zeros allowed.
The following formulae hold:
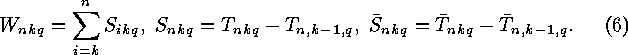
As initial values we have 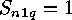 for
for  ,
,  and
and
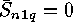 for
for  . It is important to realize that
. It is important to realize that
-
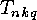 is the number of orbits of functions from
is the number of orbits of functions from  to
to
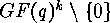 without any restrictions on the rank of the induced
matrix.
without any restrictions on the rank of the induced
matrix.
- All matrices which are induced from functions
 of the same
orbit have the same rank.
of the same
orbit have the same rank.
- The number of orbits of functions
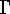 which induce matrices of
rank less or equal
which induce matrices of
rank less or equal 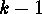 is
is  . (This proposition holds for
. (This proposition holds for 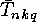 as well.)
as well.)
In the next section we will show that the 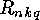 or
or 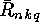 can be
computed from the
can be
computed from the 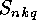 or
or 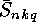 respectively, so the main
problem is the computation of the
respectively, so the main
problem is the computation of the 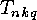 or
or 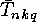 .
.
In the case 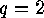 the wreath product
the wreath product 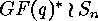 becomes the group
becomes the group
 , and so there is the group
, and so there is the group 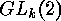 acting on
acting on 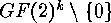 and the symmetric group
and the symmetric group  acting on
acting on  . Applying the
formulae (3) and (4) we get
. Applying the
formulae (3) and (4) we get
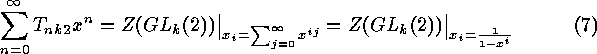
and
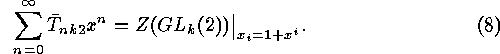
In the case  the wreath product
the wreath product 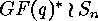 acts both on
range and domain of the functions
acts both on
range and domain of the functions 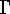 . Applying LEHMANN's
Lemma 1.1 there is the bijection
. Applying LEHMANN's
Lemma 1.1 there is the bijection
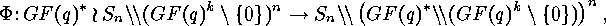

where
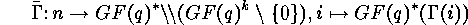
and
 acts on
acts on 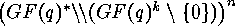 by
by 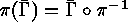 . Using this bijection we
have to investigate the following action of
. Using this bijection we
have to investigate the following action of 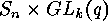 :
:
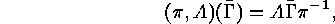
where  acts on
acts on 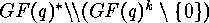 by
by
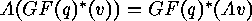 . The set of the
. The set of the 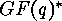 -orbits
-orbits
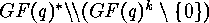 is the
is the 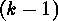 -dimensional
projective space:
-dimensional
projective space:
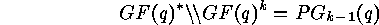
and the representation of  as a permutation group is the projective
linear group
as a permutation group is the projective
linear group 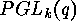 .
.
This proves in fact the following to be true:
 .
. Theorem
The isometry classes of linear
Theorem
The isometry classes of linear 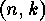 -codes over
-codes over 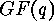 are the orbits
of
are the orbits
of 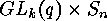 on the set of mappings
on the set of mappings  . This set of
orbits is equal to the set of orbits of
. This set of
orbits is equal to the set of orbits of  on the set
on the set 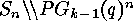 , which can be represented by a complete set of mappings of
different content, if the content of
, which can be represented by a complete set of mappings of
different content, if the content of  is defined to be
the sequence of orders of inverse images
is defined to be
the sequence of orders of inverse images 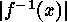 .
.
Thus the set of isometry classes of linear 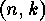 -codes over
-codes over 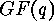 is
equal to the set of orbits of
is
equal to the set of orbits of  on the set of mappings
on the set of mappings  of different content that form
of different content that form 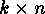 -matrices of rank
-matrices of rank
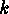 .
.
The particular classes of elements with orders of inverse images 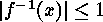 are the classes consisting of Hamming codes.
are the classes consisting of Hamming codes.
Knowing the cycle index of 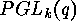 acting on
acting on 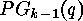 the equations
(3) and (4) can be applied again.
the equations
(3) and (4) can be applied again.
In [13] SLEPIAN explained how the cycle index of 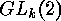 can
be computed using results of ELSPAS [3]. The first author
[4] generalized this concept for computing the cycle indices of
can
be computed using results of ELSPAS [3]. The first author
[4] generalized this concept for computing the cycle indices of
 and
and 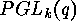 acting on
acting on 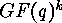 or
or 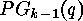 respectively.
The steps of the method used were the following ones:
respectively.
The steps of the method used were the following ones:
- Determination of the conjugacy classes of
 by applying the
theory of normal forms of matrices (or vector space endomorphisms). This
theory can be found in many textbooks of algebra.
by applying the
theory of normal forms of matrices (or vector space endomorphisms). This
theory can be found in many textbooks of algebra.
- Determination of the order of the conjugacy classes, which can be found
in DICKSON, GREEN or KUNG [8][5][2].
- Determination of the cycle type of a linear map or of a projectivity
respectively. Since normal forms of regular matrices are strongly connected
with companion and hypercompanion matrices (see [6]) of monic,
irreducible polynomials over
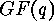 it is important to know the exponent or subexponent of such polynomials (see
[6][11]). The exponent of such a polynomial
it is important to know the exponent or subexponent of such polynomials (see
[6][11]). The exponent of such a polynomial 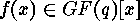 is defined to be
is defined to be 
and the subexponent is
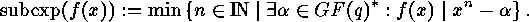
This element 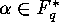 is uniquely defined, and it is called the integral element of
is uniquely defined, and it is called the integral element of 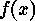 . The exponent of
. The exponent of 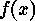 can be used to compute
the cycle type of the companion or hypercompanion matrices of a monic,
irreducible polynomial
can be used to compute
the cycle type of the companion or hypercompanion matrices of a monic,
irreducible polynomial 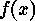 , and by a direct product formula for cycle
indices the cycle types of the normal forms in
, and by a direct product formula for cycle
indices the cycle types of the normal forms in 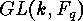 can be derived.
Using the subexponent of
can be derived.
Using the subexponent of 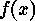 and defining a formula similar to the direct
product formula of cycle indices, which depends on the integral element of
and defining a formula similar to the direct
product formula of cycle indices, which depends on the integral element of
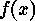 as well, the cycle type of a projectivity can be computed.
as well, the cycle type of a projectivity can be computed.
- Determination of the cycle index by applying formula ().
These cycle indices are now available in the computer algebra package
SYMMETRICA. Tables obtained this way are shown lower down.



Next: Indecomposability
Up: Isometry Classes of Indecomposable
Previous: Notation
Herr Fripertinger
Sun Feb 05 17:20:29 MET 1995
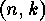 -code over the Galois field
-code over the Galois field 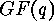 is a
is a
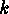 -dimensional subspace of the vector space
-dimensional subspace of the vector space  . As usual
codewords will be written as rows
. As usual
codewords will be written as rows  . A
. A 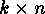 -matrix
-matrix 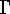 over
over 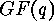 is called a generator matrix of the
linear
is called a generator matrix of the
linear 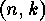 -code
-code 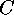 , if and only if the rows of
, if and only if the rows of 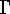 form a basis of
form a basis of
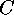 , so that
, so that 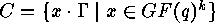 . Two linear
. Two linear
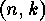 -codes
-codes 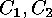 are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps
are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps  onto
onto
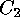 . Using the notion of finite group actions one can easily express
equivalence of codes in terms of the wreath product action introduced above:
. Using the notion of finite group actions one can easily express
equivalence of codes in terms of the wreath product action introduced above:
 and
and 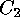 are equivalent, if and only if there exist
are equivalent, if and only if there exist  (where
(where 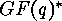 denotes the multiplicative group of the
Galois field) such that
denotes the multiplicative group of the
Galois field) such that  .
.
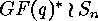 of degree
of degree  over
over
 as it was described above (see
equation (
as it was described above (see
equation ( on
on 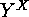 :
:
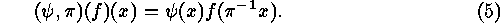
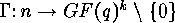 where
where 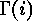 is the
is the 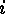 -th column of the
generator matrix
-th column of the
generator matrix  -columns for obvious reasons.)
-columns for obvious reasons.)
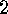 .
.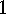 Theorem
Theorem 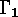 and
and 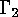 from
from 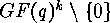 are generator matrices of two equivalent
codes, if and only if
are generator matrices of two equivalent
codes, if and only if 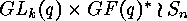 as permutation group on
as permutation group on
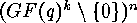 :
: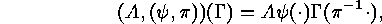
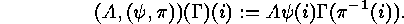
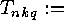
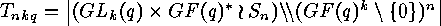 .
.
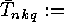
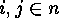 ,
, 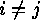 and all
and all  the value of
the value of
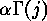 . (In the case
. (In the case 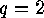 , this is
the number of injective functions
, this is
the number of injective functions 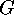 .)
.)
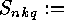
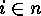 such that
such that 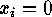 for all
codewords
for all
codewords  , and so we should exclude such columns.)
, and so we should exclude such columns.)
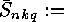
 there is some codeword
there is some codeword 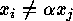 .)
.)
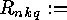

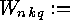
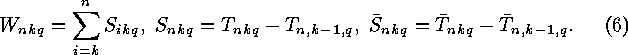
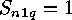 for
for 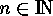 ,
, 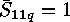 and
and
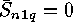 for
for  . It is important to realize that
. It is important to realize that
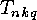 is the number of orbits of functions from
is the number of orbits of functions from 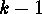 is
is  . (This proposition holds for
. (This proposition holds for 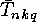 as well.)
as well.)
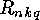 or
or 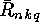 can be
computed from the
can be
computed from the 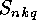 or
or 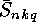 respectively, so the main
problem is the computation of the
respectively, so the main
problem is the computation of the  , and so there is the group
, and so there is the group 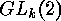 acting on
acting on 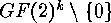 and the symmetric group
and the symmetric group 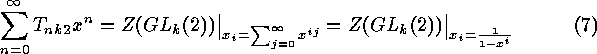
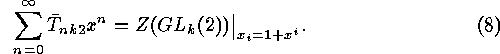
 the wreath product
the wreath product 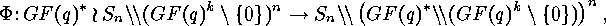

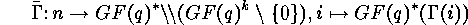
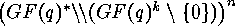 by
by 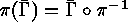 . Using this bijection we
have to investigate the following action of
. Using this bijection we
have to investigate the following action of 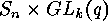 :
: 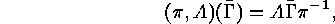
 acts on
acts on 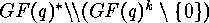 by
by
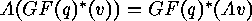 . The set of the
. The set of the 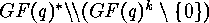 is the
is the 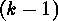 -dimensional
projective space:
-dimensional
projective space: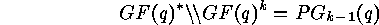
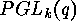 .
.
 .
. Theorem
The isometry classes of linear
Theorem
The isometry classes of linear 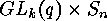 on the set of mappings
on the set of mappings  . This set of
orbits is equal to the set of orbits of
. This set of
orbits is equal to the set of orbits of 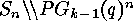 , which can be represented by a complete set of mappings of
different content, if the content of
, which can be represented by a complete set of mappings of
different content, if the content of  is defined to be
the sequence of orders of inverse images
is defined to be
the sequence of orders of inverse images 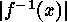 .
.
 of different content that form
of different content that form 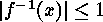 are the classes consisting of Hamming codes.
are the classes consisting of Hamming codes. 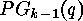 the equations
(
the equations
(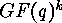 or
or 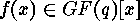 is defined to be
is defined to be 
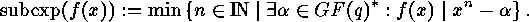
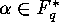 is uniquely defined, and it is called the integral element of
is uniquely defined, and it is called the integral element of 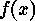 . The exponent of
. The exponent of 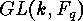 can be derived.
Using the subexponent of
can be derived.
Using the subexponent of