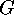 on a set
on a set 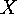 . It induces
interesting structures both on
. It induces
interesting structures both on 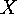 and on
and on 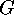 that are closely related (for
more details cf. [7]). To begin with, there are the orbits of the elements
that are closely related (for
more details cf. [7]). To begin with, there are the orbits of the elements  :
: 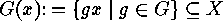 , two of which are either identical or disjoint. Therefore, the
set
, two of which are either identical or disjoint. Therefore, the
set
Suppose we are given a permutation group 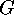 on a set
on a set 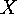 . It induces
interesting structures both on
. It induces
interesting structures both on 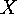 and on
and on 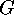 that are closely related (for
more details cf. [7]). To begin with, there are the orbits of the elements
that are closely related (for
more details cf. [7]). To begin with, there are the orbits of the elements  :
: 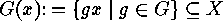 , two of which are either identical or disjoint. Therefore, the
set
, two of which are either identical or disjoint. Therefore, the
set
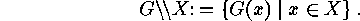
of all the orbits is a set-partition of 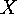 . To the orbits there
correspond the stabilizers (which are in fact subgroups):
. To the orbits there
correspond the stabilizers (which are in fact subgroups): 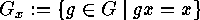 , and the close relationship between orbits and
stabilizers is the existence of the following natural bijection between an
orbit of an element and the set of left cosets of its stabilizer:
, and the close relationship between orbits and
stabilizers is the existence of the following natural bijection between an
orbit of an element and the set of left cosets of its stabilizer:

The cycle index of 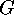 is the following polynomial
is the following polynomial  in the
indeterminates
in the
indeterminates 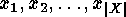 over
over 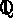 , defined by
, defined by
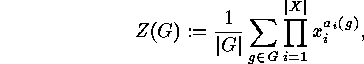
where 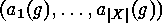 is the cycle type of the permutation
is the cycle type of the permutation
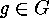 . This means,
. This means,  decomposes into
decomposes into 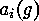 disjoint cycles of length
disjoint cycles of length
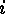 for
for 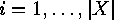 . All elements of a conjugacy class have the same
cycle type, so the cycle index can be computed in the following way:
. All elements of a conjugacy class have the same
cycle type, so the cycle index can be computed in the following way:
where 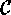 is the system of conjugacy classes of
is the system of conjugacy classes of 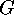 and where
and where 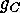 is a
representative of the conjugacy class
is a
representative of the conjugacy class 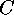 .
.
Let 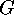 and
and  denote permutation groups on
denote permutation groups on 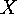 and
and 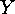 , respectively. The
wreath product
, respectively. The
wreath product  is a permutation group on the set
is a permutation group on the set
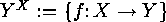 , defined by
, defined by
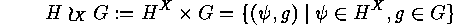
with multiplication  , where
, where
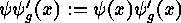 and
and  .
In the case when
.
In the case when  and
and 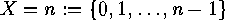 we write
we write 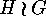 instead of
instead of 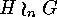 .
.
The wreath product  acts in a natural way on
acts in a natural way on 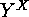 . The effect of
the permutation
. The effect of
the permutation 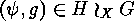 on
on 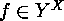 is
is
The following lemma ([9][10]) reduces the action of a wreath
product to the action of the group 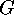 on the set of all functions from
on the set of all functions from 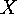 into the set of all orbits of
into the set of all orbits of  on
on 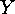 :
:
Moreover, the mapping
is a bijection if 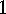 .
. Lehmann's Lemma:
If
Lehmann's Lemma:
If 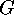 and
and  denote permutation groups on
denote permutation groups on 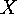 and
and 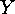 , respectively,
then
, respectively,
then 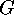 acts on
acts on 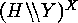 in the following way:
in the following way:

 is given by
is given by 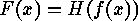 .
.
There are many enumerative and constructive results dealing with various
group actions on the set 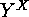 induced by permutation groups on the domain
induced by permutation groups on the domain
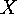 and on the range
and on the range 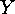 . For example,
. For example, 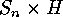 acts upon
acts upon 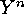 by
by
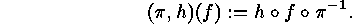
The corresponding generating function for the numbers of 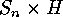 -orbits on
-orbits on 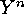 is given by (see [1]):
is given by (see [1]):
The group action of above can be restricted to the set of all injective
mappings from  to
to 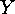 , the corresponding generating function is
, the corresponding generating function is