The result in ![]() is very important, it is
essential in the proof of
the following counting lemma which, together with later refinements,
forms the basic tool of the theory of enumeration under finite group
action:
is very important, it is
essential in the proof of
the following counting lemma which, together with later refinements,
forms the basic tool of the theory of enumeration under finite group
action:
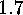 .
.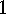 The Lemma of Cauchy-Frobenius
The number of orbits of a finite group
The Lemma of Cauchy-Frobenius
The number of orbits of a finite group  acting on a finite set
acting on a finite set 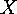 is equal to the average
number of fixed points:
is equal to the average
number of fixed points:
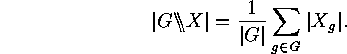
Proof:
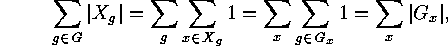

Now you can try to make some calculations using the Cauchy-Frobenius Lemma.