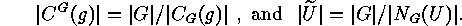and the set of left cosets of its stabilizer:
and the set of left cosets of its stabilizer:
Returning to the general case we first state the main
(and obvious) properties of the stabilizers of elements belonging to
the same orbit:
But the crucial point is the following
natural bijection between the orbit
of  and the set of left cosets of its stabilizer:
and the set of left cosets of its stabilizer:
 .
. Lemma
The mapping
Lemma
The mapping 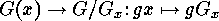 is a
bijection.
is a
bijection.
Proof: It is clear from ![]() that, for a given
that, for a given 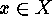 , the following
chain
of equivalences
holds:
, the following
chain
of equivalences
holds:
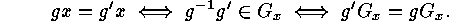
Reading it from left to right we see that 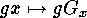 defines a mapping,
reading it from right to left we obtain that it is injective. Furthermore
it is obvious that this mapping is also surjective.
defines a mapping,
reading it from right to left we obtain that it is injective. Furthermore
it is obvious that this mapping is also surjective.

This result shows in particular that the length of the orbit is the index of the stabilizer, so that we obtain
 .
.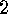 Corollary
If
Corollary
If  is a finite group acting on the set
is a finite group acting on the set 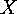 , then for each
, then for each 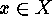 we
have
we
have


An application to the examples given above yields:
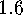 .
.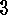 Corollary
If
Corollary
If  is finite,
is finite, 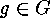 , and
, and 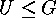 , then the orders of the conjugacy
classes of elements and of subgroups satisfy the following equations:
, then the orders of the conjugacy
classes of elements and of subgroups satisfy the following equations: