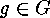 by a summation over a transversal
of the conjugacy classes,
as the number of fixed points turns out to be constant on each such
class:
by a summation over a transversal
of the conjugacy classes,
as the number of fixed points turns out to be constant on each such
class:
The next remark helps considerably to shorten the calculations necessary
for applications of this lemma. It shows that we can replace the summation
over all 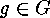 by a summation over a transversal
of the conjugacy classes,
as the number of fixed points turns out to be constant on each such
class:
by a summation over a transversal
of the conjugacy classes,
as the number of fixed points turns out to be constant on each such
class:
is a bijection, and hence
is a class function ,
i.e. it is constant
on the conjugacy classes of 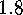 .
. Lemma
The mapping
Lemma
The mapping
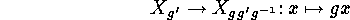
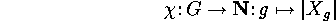
 . More formally, for any
. More formally, for any  ,
we have that
,
we have that
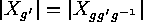 .
.
Proof: That  establishes a bijection between
establishes a bijection between 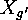 and
and
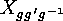 is clear from the following equivalence:
is clear from the following equivalence:
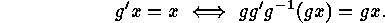

The mapping
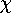 is called the character
of the action of
is called the character
of the action of  on
on 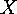 ,
or of
,
or of  , in short.
, in short.