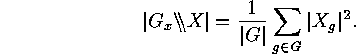 .
. Corollary
Let
Corollary
Let 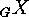 be a finite action and let
be a finite action and let 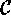 denote a
transversal of the conjugacy classes of G. Then
denote a
transversal of the conjugacy classes of G. Then
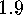 .
. Corollary
Let
Corollary
Let 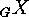 be a finite action and let
be a finite action and let 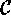 denote a
transversal of the conjugacy classes of G. Then
denote a
transversal of the conjugacy classes of G. Then
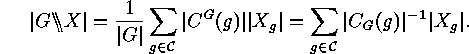
Here is the faster version of the Cauchy-Frobenius Lemma.
Another formulation of the Cauchy-Frobenius Lemma makes use of the
permutation representation 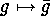 defined by the action
in question. (Actually in all our programs we apply this version of the Lemma.)
The permutation group
defined by the action
in question. (Actually in all our programs we apply this version of the Lemma.)
The permutation group 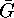 which is the image of
which is the image of  under this representation, yields the action
under this representation, yields the action 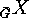 of
of 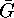 on
on 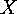 ,
which has the
same orbits, and so
we also have:
,
which has the
same orbits, and so
we also have:
where
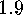 .
.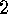 Corollary
If
Corollary
If 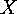 denotes a finite
denotes a finite  -set, then (for
any group
-set, then (for
any group  ) the following identity holds:
) the following identity holds:
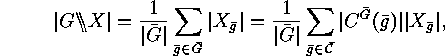
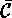 denotes a transversal of the conjugacy classes of
denotes a transversal of the conjugacy classes of 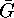 .
.
Exercises
E  .
. Let
Let 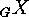 be finite and transitive. Consider an
arbitrary
be finite and transitive. Consider an
arbitrary 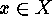 and prove that
and prove that