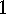Involutions




Next: The Involution Principle
Up: Actions
Previous: Selfcomplementary graphs
Before we generalize this method of complementation we should recall  .
It shows that each action of the form
.
It shows that each action of the form
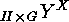 can be considered as an action of
can be considered as an action of  on
on 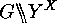 or
as an action of
or
as an action of  on
on 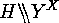 . Hence each such action of
. Hence each such action of
 on
on 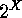 gives rise to an action of
gives rise to an action of 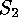 on
on
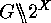 and leads us to the discussion of the Involution
Principle.
We call a group element
and leads us to the discussion of the Involution
Principle.
We call a group element 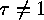 an involution
if and only if
an involution
if and only if 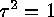 . The Involution Principle is a method of counting objects by simply
defining a nice involution
. The Involution Principle is a method of counting objects by simply
defining a nice involution  on a suitably chosen set
on a suitably chosen set 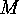 and using
the fact that
and using
the fact that 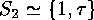 has orbits of length 1 (the
selfenantiomeric orbits) and of length 2 (which form the enantiomeric pairs)
only. A typical example is the complementation
has orbits of length 1 (the
selfenantiomeric orbits) and of length 2 (which form the enantiomeric pairs)
only. A typical example is the complementation  of graphs
which is, for
of graphs
which is, for 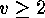 , an involution on the set of graphs on
, an involution on the set of graphs on  vertices. An even easier case
is described in
vertices. An even easier case
is described in
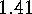 .
. Examples We wish to
prove that the number of divisors
of
Examples We wish to
prove that the number of divisors
of 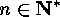 is odd if and only if
is odd if and only if 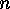 is a square. In order to do
this we consider the set
is a square. In order to do
this we consider the set 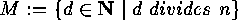 of
these divisors and define
of
these divisors and define
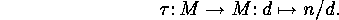
This mapping
is an involution, if  , and obviously
, and obviously 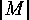 is odd if and only if
is odd if and only if
 has a fixed point, i.e. if and only if
there exists a divisor
has a fixed point, i.e. if and only if
there exists a divisor 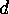 such that
such that 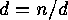 , or,
in other words, if and only if
, or,
in other words, if and only if 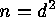 .
.
A less trivial example is the following proof (due to D. Zagier) of the fact
that every prime number which is congruent 1 modulo 4 can be expressed as
a sum of two squares of positive natural numbers. Consider the set
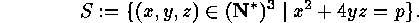
The following map is an involution on 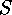 (exercise
(exercise  ):
):
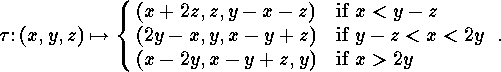
This involution has exactly one fixed point, namely 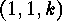 , if
, if 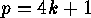 ,
therefore
,
therefore 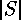 must be odd, and consequently the involution
must be odd, and consequently the involution

possesses a fixed point, too, which shows that 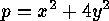 , a sum of two
squares.
, a sum of two
squares.

Exercises
E 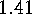 .
.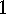 Check the details of the second example in
Check the details of the second example in  .
.




Next: The Involution Principle
Up: Actions
Previous: Selfcomplementary graphs
Herr Fripertinger
Sun Feb 05 18:28:26 MET 1995
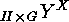 can be considered as an action of
can be considered as an action of  on
on 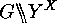 or
as an action of
or
as an action of  on
on 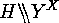 . Hence each such action of
. Hence each such action of
 on
on 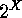 gives rise to an action of
gives rise to an action of 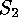 on
on
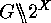 and leads us to the discussion of the Involution
Principle.
We call a group element
and leads us to the discussion of the Involution
Principle.
We call a group element 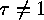 an involution
if and only if
an involution
if and only if 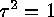 . The Involution Principle is a method of counting objects by simply
defining a nice involution
. The Involution Principle is a method of counting objects by simply
defining a nice involution  on a suitably chosen set
on a suitably chosen set 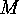 and using
the fact that
and using
the fact that 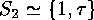 has orbits of length 1 (the
selfenantiomeric orbits) and of length 2 (which form the enantiomeric pairs)
only. A typical example is the complementation
has orbits of length 1 (the
selfenantiomeric orbits) and of length 2 (which form the enantiomeric pairs)
only. A typical example is the complementation  of graphs
which is, for
of graphs
which is, for 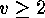 , an involution on the set of graphs on
, an involution on the set of graphs on  vertices. An even easier case
is described in
vertices. An even easier case
is described in
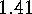 .
. Examples
Examples 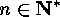 is odd if and only if
is odd if and only if 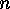 is a square. In order to do
this we consider the set
is a square. In order to do
this we consider the set 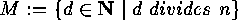 of
these divisors and define
of
these divisors and define
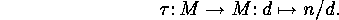
 , and obviously
, and obviously  is odd if and only if
is odd if and only if
 such that
such that 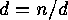 , or,
in other words, if and only if
, or,
in other words, if and only if 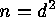 .
.
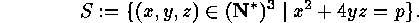
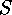 (exercise
(exercise 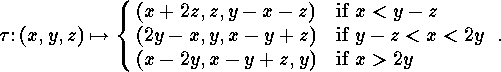
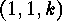 , if
, if 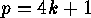 ,
therefore
,
therefore 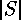 must be odd, and consequently the involution
must be odd, and consequently the involution

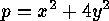 , a sum of two
squares.
, a sum of two
squares.

 .
.