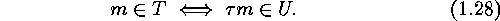
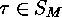be an involution which has the following reversion
property with respect to the subsets 
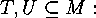
Then the restriction of 
to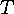 
establishes a bijection between 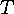and
.
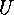We shall apply this to disjoint
decompositions 
of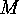 
into
subsets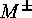 
. Each such disjoint decomposition gives rise to a
sign function on :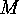
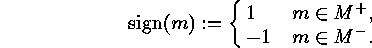
Then the the restriction of
If in addition 
.
The Involution Principle Let be a disjoint
decomposition of a finite set 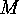and let 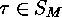be a sign
reversing involution:
to 
is a bijection
onto 
. Moreover
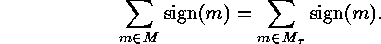
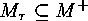, then
Proof:
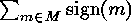is equal to
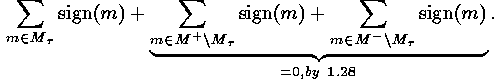
Exercises
E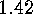 
.
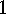Assume 
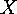to be a finite set with subsets 
. Use the
Principle of Inclusion and Exclusion in order to derive the number of
elements of 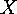which lie in precisely 
of these subsets 
.
