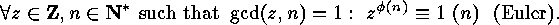According to ![]() we obtain from
we obtain from ![]() the following results:
the following results:
and also
as well as
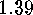 .
. Corollary
For any subgroups
Corollary
For any subgroups 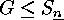 and
and 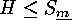 , the following congruences
hold:
, the following congruences
hold:
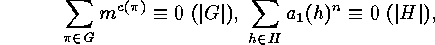
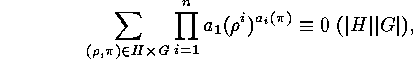
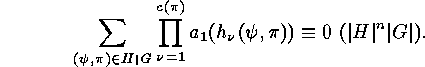
Further congruences show up in the enumeration of group elements with
prescribed properties. This theory of enumeration in finite groups is,
besides the enumeration of chemical graphs, one of the main sources for
the theory of enumeration which we are discussing here. A prominent example
taken from this complex of problems is the following one due to
Frobenius: The number of solutions of the equation 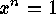 in a finite
group
in a finite
group  is divisible by
is divisible by 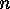 , if
, if 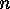 divides the order of
divides the order of  . There
are many proofs of this result and also many generalizations. Later on we
return to this problem, at present we can only discuss a particular
case which can be treated with the tools we
already have at hand.
. There
are many proofs of this result and also many generalizations. Later on we
return to this problem, at present we can only discuss a particular
case which can be treated with the tools we
already have at hand.
 .
.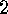 Example
Let
Example
Let 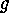 denote an element of a finite group which forms its own conjugacy
class and consider a prime number
denote an element of a finite group which forms its own conjugacy
class and consider a prime number  , which divides
, which divides 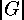 . We
want to show that the number of solutions
. We
want to show that the number of solutions 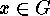 of the equation
of the equation
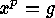 is divisible by
is divisible by  .
In order to prove this we consider the action of
.
In order to prove this we consider the action of 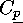 on the set
on the set 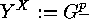 . The orbits are of length 1 or
. The orbits are of length 1 or  .
An orbit is of length 1 if and only if
it consists of a single and therefore of a constant mapping
.
An orbit is of length 1 if and only if
it consists of a single and therefore of a constant mapping
 , say. We now restrict our attention to the following subset
, say. We now restrict our attention to the following subset
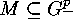 :
:
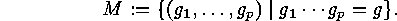
As 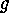 forms its own conjugacy class, we obtain a subaction of
forms its own conjugacy class, we obtain a subaction of 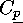 on
on 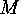 (for example
(for example 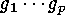 is conjugate to
is conjugate to  ).
Hence the desired number
).
Hence the desired number 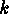 of solutions of
of solutions of 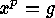 is equal to
the number of orbits of length 1 in
is equal to
the number of orbits of length 1 in 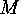 . Now we consider the number
. Now we consider the number 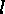 of
orbits of length
of
orbits of length  in
in 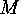 . It satisfies the equation
. It satisfies the equation
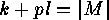 . As each equation
. As each equation 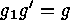 has a unique
solution
has a unique
solution 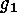 in
in  , we moreover have that
, we moreover have that
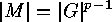 . Thus
. Thus
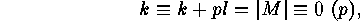
which completes the proof.
We note in passing that the center of  consists
of the elements which
form their own conjugacy class, so that we have proved the following:
consists
of the elements which
form their own conjugacy class, so that we have proved the following:
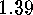 .
.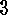 Corollary
If the prime
Corollary
If the prime  divides the order of the
group
divides the order of the
group  , then the number of
, then the number of  -th roots of each element in the center of
-th roots of each element in the center of
 is divisible by
is divisible by  .
In particular the number of
.
In particular the number of  -th roots of the
unit element
-th roots of the
unit element 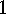 of
of  has this property (and it is nonzero, since
has this property (and it is nonzero, since 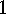 is
a
is
a  -th root of
-th root of 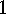 ), and hence
), and hence  contains elements of
order
contains elements of
order  .
.
This result can be used in order to give an inductive proof of Sylow's
Theorem which we proved in example ![]() .
.

Exercises
E 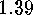 .
. Prove, by considering suitable actions, the following facts:
Prove, by considering suitable actions, the following facts:
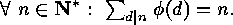
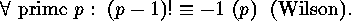
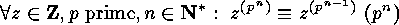 .
.