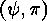 in
in 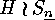 and assume that
and assume that
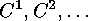 are the conjugacy classes of
are the conjugacy classes of  . If
. If
Consider an element 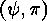 in
in 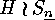 and assume that
and assume that
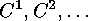 are the conjugacy classes of
are the conjugacy classes of  . If
. If
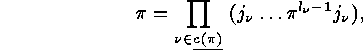
in standard cycle notation, then we associate with its  -th cyclic factor
-th cyclic factor
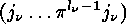 the element
the element
of  and call it the
and call it the  -th cycleproduct of
-th cycleproduct of 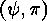 or the
cycleproduct associated to
or the
cycleproduct associated to 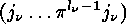 with respect to
with respect to 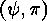 . In this way we obtain a total of
. In this way we obtain a total of
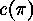 cycleproducts,
cycleproducts,
 of them arising from the cyclic factors of
of them arising from the cyclic factors of  which are of length
which are of length 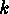 . Now let
. Now let 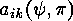 be the number of these
cycleproducts which are associated to a
be the number of these
cycleproducts which are associated to a 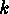 -cycle of
-cycle of  and which belong
to the conjugacy class
and which belong
to the conjugacy class 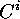 of
of  (note that we did not
say
let
(note that we did not
say
let 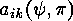 be the number of different cycleproducts ).
We
put these natural numbers together into the matrix
be the number of different cycleproducts ).
We
put these natural numbers together into the matrix
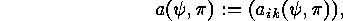
This matrix has 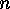 columns (
columns (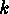 is the column index)
and as many rows as there are conjugacy classes
in
is the column index)
and as many rows as there are conjugacy classes
in  (
( is the row index). Its entries satisfy the following conditions:
is the row index). Its entries satisfy the following conditions:
We call this matrix 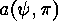 the type
of
the type
of 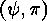 and we say that
and we say that 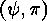 is of type
is of type 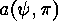 .
.
occurs as the type of an element
where 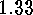 .
. Lemma
The conjugacy classes of
complete monomial groups
Lemma
The conjugacy classes of
complete monomial groups 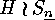 have the following properties:
have the following properties:
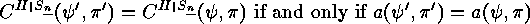 .
.
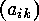 in
in
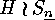 ,
,  finite, is equal to
finite, is equal to
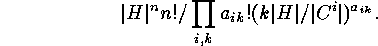
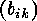 with
with 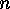 columns and as many rows as
columns and as many rows as  has
conjugacy classes, the elements of which satisfy
has
conjugacy classes, the elements of which satisfy
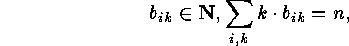
 .
.
 is a permutation group and
is a permutation group and 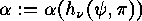 , then the cycle partition
, then the cycle partition 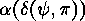 , where
, where
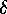 denotes the permutation representation of
denotes the permutation representation of ![]() ,
is equal
to
,
is equal
to

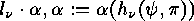 , is defined to be
, is defined to be
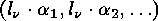 , and where
, and where 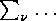 means that the proper partition has to be formed that consists of all the
parts of all the summands
means that the proper partition has to be formed that consists of all the
parts of all the summands 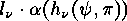 .
.
Proof: A first remark concerns the cycleproducts introduced in ![]() . Since
in each group
. Since
in each group  the products
the products  and
and 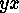 of two elements are conjugate, we
have that
of two elements are conjugate, we
have that
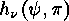 is conjugate to
is conjugate to
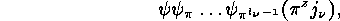
for each integer  .
.
The second remark is, that for each 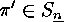 and every
and every 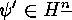 ,
,
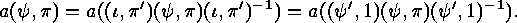
This follows from the fact that both 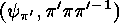 and
and
 are of type
are of type 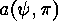 .
.
A third remark is that 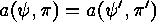 implies the existence of an
element
implies the existence of an
element 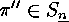 which satisfies
which satisfies 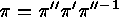 , and for which
the cycleproducts
, and for which
the cycleproducts 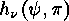 and
and  are
conjugate.
are
conjugate.
It is not difficult to check these remarks and then to derive the statement
(exercise ![]() ).
).

Exercises
E 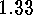 .
. Prove that the conjugacy class (in
Prove that the conjugacy class (in  ) of an even element
) of an even element 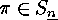 splits into two
splits into two 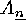 -classes if and only if
the lengths of the
cyclic factors of
-classes if and only if
the lengths of the
cyclic factors of  are pairwise different and odd (hint: use
are pairwise different and odd (hint: use ![]() ).
).
E  .
. Fill in the details of the proof of
Fill in the details of the proof of ![]() .
.