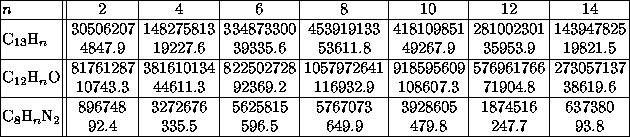
Der zweite Approximationsschritt im Rahmen der molekularen Strukturerkennung
besteht darin, zu einer Summenformel alle zusammenhängenden
Graphen zu konstruieren, die die entsprechende Eckengrad- (=Valenzen-) Folge
haben,
weitere Zusatzbedingungen erfüllen (wie etwa eine Hydroxylgruppe -OH
enthalten, wenn es sich um Alkohole handeln soll),
und zusätzlich noch hierzu alle Färbungen der Punkte dieser Graphen mit den
richtigen Atomnamen vorzunehmen, und zwar redundanzfrei und schnell! Daß
dies kein einfaches Problem ist, zeigt schon die folgende Tabelle, die
einige Anzahlen samt Rechenzeiten (auf einem PC mit 486DX2-66) angibt:
MOLGEN berechnet alle (mathematisch) möglichen Bindungsisomere zu einer gegebenen Summenformel mit Nebenbedingungen, führt also diesen zweiten Approximationsschritt bei der Molekularen Strukturerkennung durch, indem es schnell und redundanzfrei die vollständige Varietät aller zu den (graphischen, aus den spektroskopischen Daten gewonnenen) Ausgangsdaten passenden Bindungsisomere bereitstellt. Dabei werden drei Listen von Substrukturen verwendet: Makroatome, Goodlist und Badlist. Darüber hinaus sind weitere Restriktionen wie Ringbeschränkungen, max. Bindungsgrad möglich, um die Menge der resultierenden Isomere weiter zu reduzieren.
H
O
mehr als eine Milliarde mathematisch möglicher Strukturformeln, d.h.
molekulare Graphen,
gibt. Sofort entsteht die Frage --- auch angesichts der "nur"
ca. 10 Millionen bisher registrierter chemischer
Substanzen ---, ob diese alle existieren können. Dazu ist zu sagen, daß es
graphische Nebenbedingungen gibt, die Isomere verhindern, die allgemein als
instabil angesehen werden. Hat man diese Bedingungen eingeben (in einer
sogenannten permanenten Badlist), so erhält man zu dem angegebenen
Molekül
deutlich weniger, aber oft immer noch sehr viele Bindungsisomere.
Für C
H
resultieren --- bzgl. einer von Chemikern gelegentlich
benutzten solchen Liste verbotener Substrukturen ---
statt 217 nur noch 87 Isomere, eine gute Approximation der bisher
nachgewiesenen ca. 70. Bei der einen Formel C
H
O bleiben von der
einen Milliarde
aus der obigen Tabelle immer noch mehr Isomere übrig als es bei CAS bisher
registrierte chemische Substanzen mit beliebigen Formeln insgesamt gibt,
was die enorm groß e Vielfalt der Möglichkeiten sehr
anschaulich demonstriert.
Die beim Entwurf von MOLGEN verwandten mathematischen
Methoden sind eine Mischung aus algebraischen
(insbesondere auch gruppentheoretischen) und kombinatorischen Algorithmen
(für Einzelheiten vgl. [6,10,12,20]).
Die Farbtafel II zeigt als Beispiel
die Berechnung der 22 Bindungsisomere des Dioxin, also die Bindungsisomere
zur chemischen Formel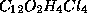 
mit der vorgeschriebenen Substruktur
"dioxin", die die folgende Form hat:
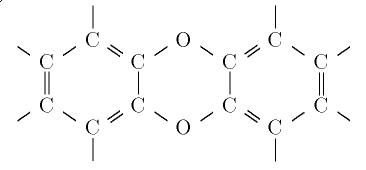
An diesem Beispiel können wir eine der benutzten gruppentheoretischen
Methoden gut illustrieren und zeigen, wie diese zur wesentlichen
Verminderung der Komplexität beitragen können. Es handelt sich dabei
nämlich um sogenannte Permutationsisomere, die schon E. Ruch und
Mitarbeiter in Zusammenhang mit Doppelnebenklassen gebracht
haben ([15,16]). Wir verwenden das
Dioxinskelett als Makrostruktur und lassen MOLGEN die Anzahl der
zusammenhängenden Graphen berechnen, die die übrigen Atome enthalten,
also aus dem Makroatom 
und 4 Wasserstoff sowie 4 Chloratomen
bestehen. Hierzu
gibt es natürlich genau einen Graphen:
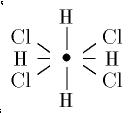
Wenn wir jetzt den zentralen Knoten dieses Graphen zum Dioxinskelett "aufblasen", dann besteht das Problem darin, die acht freien Valenzen des Dioxinskeletts mit den acht Kanten des sternförmigen Graphen dergestalt zu identifizieren, daß nur die wesentlich verschiedenen unter diesen Identifizierungen auftreten, aber auch jede einmal vorkommt. Man kann zeigen, daß diese Identifizierungen zu einer Transversale der Menge
(
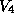die Kleinsche Vierergruppe, auf den acht freien Valenzen, 
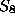die
symmetrische Gruppe hierauf,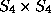 
das direkte Produkt der
symmetrischen Gruppen auf den H- bzw. auf den Cl-Atomen) von
Doppelnebenklassen bijektiv ist. Die 22 Isomere des Dioxin mit obiger
Substruktur kann man deshalb aus einer Transversale dieser Menge von
Doppelnebenklassen erhalten.
Diese Methode der Verwendung der Makroatome als Knoten mit nachfolgendem Aufblasen hat sich als sehr zweckmäß ig erwiesen, denn mit ihrer Hilfe läß t sich die Graphengenerierung auf wesentlich kleinere Graphen beschränken und damit stark beschleunigen. Im Falle des Dioxins werden Graphen mit 22 Punkten durch Graphen mit 5 Punkten ersetzt! Die weiteren Schritte bei der Behandlung des Dioxin zeigt die Farbtafel.
Zusätzliche Möglichkeiten, die MOLGEN bietet, sind das Herausfiltern aromatischer Doubletten, der Export in das weitverbreitete MolFile-Format, die Bearbeitung mit dem eingebauten Struktureditor zur interaktiven Beschränkung des Lösungsraums und die Berechnung räumlicher Plazierungen nach [1].
Ausgehend einzig von den Bindungsverhältnissen ist MOLGEN auch in der Lage, weitere räumliche Eigenschaften, nämlich alle Konfigurationsisomere zu berechnen [13,20,17,18].
Dabei werden alle wichtigen Effekte berücksichtigt: Asymmetrische
vierwertige Atome (auch in Ringen), cis/trans-Isomerie an Doppelbindungen,
Spirane sowie chirale und diastereomere Allene.
Mathematisch gesehen handelt es sich dabei um die Berechnung der Transversale
einer Gruppenoperation, nämlich der sog.
Konfigurationssymmetriegruppe
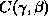, welche eine Untergruppe des Kranzproduktes
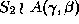mit der Automorphismengruppe 
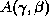ist, auf den Abbildungen 
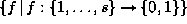bei s
Stereozentren.
Eine ausführliche Tabelle stellt
die Zahlen der Strukturisomere denen der Konfigurationsisomere gegenüber.
Diese Verhältnisse können auch graphisch veranschaulicht werden.
Zu allen Konfigurationsisomeren werden anschließend räumliche Plazierungen geometrisch durch Spiegelungen der Referenzplazierung ermittelt [17] (s. die Abbildung mit den Stereoisomeren des 1,2,3,4-Tetramethylcyclobutan).
