The permutation group ![]() is represented as the factor group
is represented as the factor group
![]() , where
, where
![]() consists of all
non-zero multiples of the identity matrix. It is much easier to handle a
consists of all
non-zero multiples of the identity matrix. It is much easier to handle a
![]() -matrix than a permutation of length
-matrix than a permutation of length ![]() , since we can apply
linear algebra to matrix problems.
We therefore represent subgroups of
, since we can apply
linear algebra to matrix problems.
We therefore represent subgroups of ![]() by the matrices which generate
them modulo
by the matrices which generate
them modulo ![]() .
.
Theorem 7
Up to conjugation in ![]() there are the following stabilizers and the
corresponding numbers of orbits of 6-sets. Here
there are the following stabilizers and the
corresponding numbers of orbits of 6-sets. Here
![]() are chosen
such that
are chosen
such that
![]() and
and ![]() has order 5 if
has order 5 if ![]() .
.
Proof
A subgroup ![]() of
of ![]() is generated by
is generated by

There is just one orbit with this stabilizer on 6-sets.
A representative is the set
![]() .
.
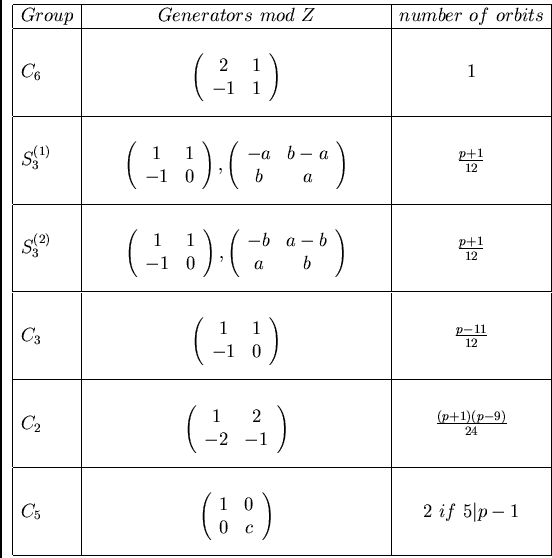
The 5-orbit covered by these 6-sets has as a stabilizer
in ![]() the subgroup of order 2 generated by
the subgroup of order 2 generated by

The matrices
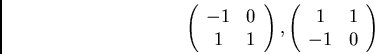
The matrices
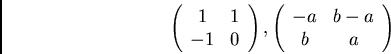
By conjugating the matrix


The matrices
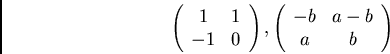
The last two subgroups isomorphic to ![]() are not conjugate in
are not conjugate in ![]() .
So, they are stabilizers of 6-sets from different orbits. The normalizer
in
.
So, they are stabilizers of 6-sets from different orbits. The normalizer
in ![]() of each of the two subgroups is generated by
of each of the two subgroups is generated by ![]() and the chosen
subgroup. They have index 2 in their normalizer such that the 6-sets
invariant under one such
and the chosen
subgroup. They have index 2 in their normalizer such that the 6-sets
invariant under one such ![]() fall into pairs that are mapped onto each other
under the action of the normalizer. By the homomorphism prinziple, these
pairs represent the orbits of
fall into pairs that are mapped onto each other
under the action of the normalizer. By the homomorphism prinziple, these
pairs represent the orbits of ![]() on 6-sets with stabilizer conjugate
to the chosen
on 6-sets with stabilizer conjugate
to the chosen ![]() .
.
All the listed elements modulo the center normalize the subgroup ![]() of
of ![]() generated by
generated by

The subgroup ![]() of order 3 of
of order 3 of ![]() is generated by
is generated by

We have to subtract those 6-sets first that are invariant under a
subgroup of order 6 containing our ![]() .
We have to subtract those
.
We have to subtract those ![]() which are invariant under
which are invariant under ![]() .
Each of the two
.
Each of the two ![]() has
has ![]() subgroups conjugate to it in the normalizer of
our
subgroups conjugate to it in the normalizer of
our ![]() , which is a dihedral group of order
, which is a dihedral group of order ![]() .
So, we for these groups have to subtract 2 times
.
So, we for these groups have to subtract 2 times ![]() times
times ![]() 6-sets.
We are left with
6-sets.
We are left with

The subgroup of order 2 of ![]() is generated by
is generated by

This element also represents the only conjugacy class
of elements of order 2 in ![]() . Let us call the
subgroup it generates
. Let us call the
subgroup it generates ![]() . Then
. Then ![]() has
has ![]() orbits of
length 2. Any 6-set invariant under
orbits of
length 2. Any 6-set invariant under ![]() is formed by selecting
3 of these orbits. We apply Lemma 4 to determine the number of orbits
of
is formed by selecting
3 of these orbits. We apply Lemma 4 to determine the number of orbits
of ![]() on 6-sets where
on 6-sets where ![]() is a stabilizer of some representative.
We first have to subtract the 6-sets that are invariant under any
larger group. So, we have to subtract the
is a stabilizer of some representative.
We first have to subtract the 6-sets that are invariant under any
larger group. So, we have to subtract the ![]() 6-sets invariant under
6-sets invariant under ![]() .
Since all conjugates of
.
Since all conjugates of ![]() have trivial intersection, our
have trivial intersection, our ![]() lies in only
one
lies in only
one ![]() .
There are 6-sets with a stabilizer of type
.
There are 6-sets with a stabilizer of type ![]() and
and ![]() is contained in some
of these, because any subgroup of order 2 of an
is contained in some
of these, because any subgroup of order 2 of an ![]() is conjugate to
is conjugate to ![]() .
As a group of order 6 each such
.
As a group of order 6 each such ![]() has
has ![]() invariant 6-sets, namely its orbits.
We now have to find out the number
invariant 6-sets, namely its orbits.
We now have to find out the number
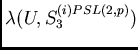 of conjugates of
of conjugates of ![]() for
for ![]() that contain
that contain ![]() .
This can be done by doubly counting the set
.
This can be done by doubly counting the set
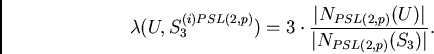
The normalizer of ![]() is a dihedral group
is a dihedral group ![]() of order
of order ![]() and
the normalizer of
and
the normalizer of
 has order 12.
So,
has order 12.
So,
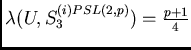 for each
for each ![]() .
By this we get the number of 6-sets with stabilizer
.
By this we get the number of 6-sets with stabilizer ![]() .
The number of orbits of
.
The number of orbits of ![]() on them is simply obtained by dividing by
the length of each orbit which is
on them is simply obtained by dividing by
the length of each orbit which is
![]() .
.
So, we get
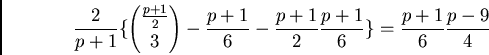
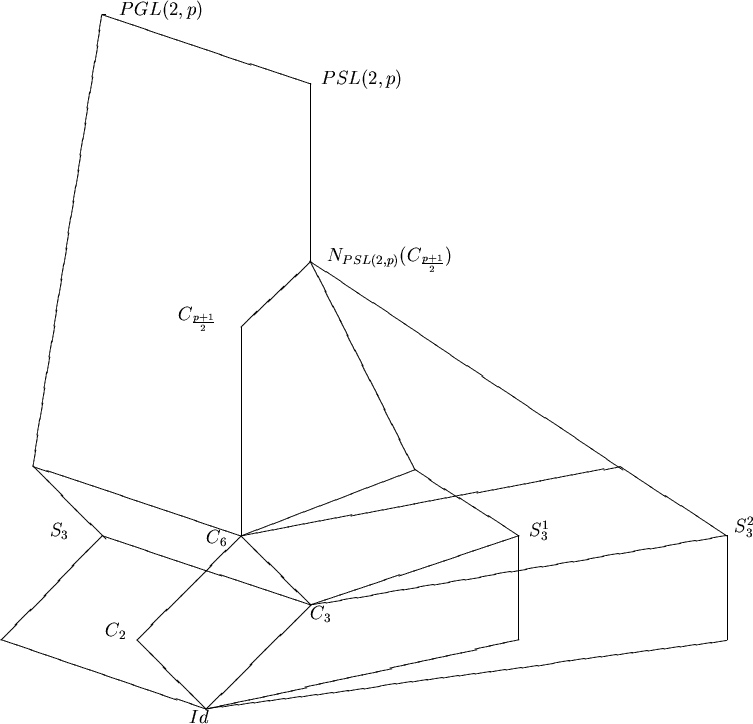
We illustrate some part of the subgroup lattice by the following picture.
While the counting of orbits is completely solved in this way the construction of orbit
representatives still needs some work. We have to find out whether a 6-set ![]() invariant under a subgroup
invariant under a subgroup ![]() has
has ![]() as its full set stabilizer. In the case of Steiner
systems this can be done by the computation of
as its full set stabilizer. In the case of Steiner
systems this can be done by the computation of
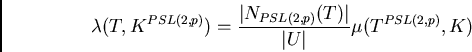
There are two possible reasons for such a value.
At first, ![]() may be contained in more than 1 block of the
orbit
may be contained in more than 1 block of the
orbit ![]() . Then this orbit cannot be in a Steiner system.
The second reason is that
. Then this orbit cannot be in a Steiner system.
The second reason is that
![]() may not be the full
stabilizer of
may not be the full
stabilizer of ![]() . So, in a consideration of all representatives
of subgroups as possible stabilizers of some block a conjugate
of
. So, in a consideration of all representatives
of subgroups as possible stabilizers of some block a conjugate
of
![]() will occur stabilizing some block in
will occur stabilizing some block in ![]() .
.