Prof. Dr. R.
Laue
WS03/04
Konstruktions Algorithmen
Übungsblatt 1
Abgabe: 3. 11.03 vor der Vorlesung
URL: /axel/konsalg_ws0304_blatt1.html
alleine bearbeiten!
Aufgabe 1 (2+4 Punkte)
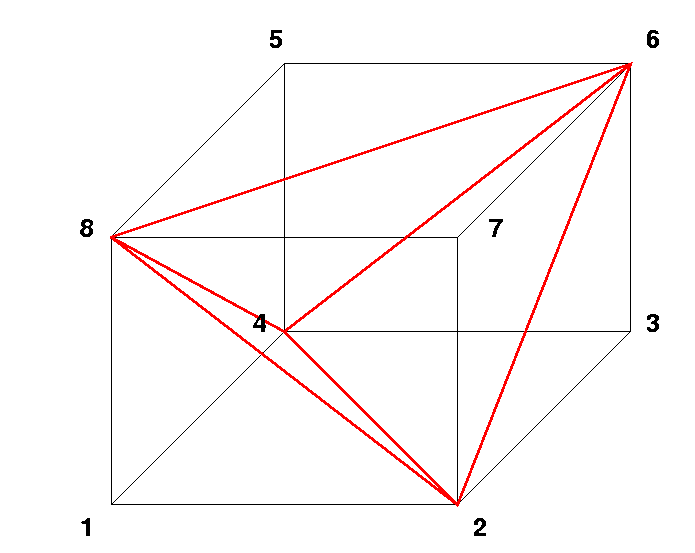
In der Vorlesung wurde gezeigt wie man durch Einbettung des Tetraeders
in den Würfel eine Untergruppe der Drehungsgruppe, die
den Würfel in sich überführt, bekommt. Diese
Untergruppe liefert ein Darstellung der Automorphismen des Tetraeders
als Permutationsgruppe vom Grad 8 (=Anzahl der Ecken des Würfels).
Geben Sie Erzeuger dieser Permutationsgruppe vom Grad 8 an.
Begründen Sie die Erzeugereigenschaft.
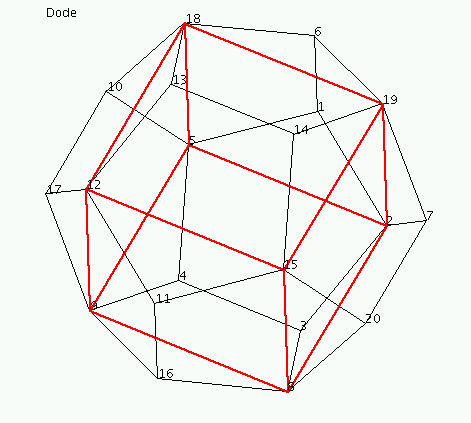
Nun kann man diesen Würfel in den Dodekaeder einbetten (dazu setzt
man Walmdächer auf die Würfelflächen) Siehe
hierzu folgendes Bild,
oder auch diesen Film.
("vom Würfel zum Icosaeder") Damit hat man dann eine Einbettung
des in den Würfel eingebetteten Tetraeders in den Dodekaeder,
geben Sie wiederum Erzeuger dieser Permutationsgruppe vom Grad 20
(Anzahl Knoten des Dodekaeders) an.