URL:
/axel/informatik1_ws0304_blatt8.html
Dieses Übungsblatt ist in Zweiergruppen zu
bearbeiten. Auf dem Blatt bitte Übungsgruppentag angeben. Um
den Übungsschein zu erhalten, muß man 50% der Punkte
erreichen
und aktiv am Übungsbetrieb teilnehmen. D.h Vorrechnen, Bearbeitung
von mindestens 80% der Übungsblätter.
Jede Aufgabe auf einem eigenen Blatt (mit Namen und Gruppe und
Matrikelnummern). Nicht mit Bleistift bearbeiten.
Aufgabe 23 - Schachcomputer - (2+4+2+2+3+3+4+2 Punkte)
Wir bauen einen Schachcomputer für Weihnachten. Es ist folgende Stellung gegeben: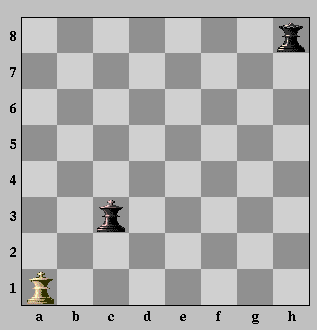
Dabei ist Weiß am Zug.
a) Zeigen Sie wie Schwarz gewinnt. (2 Punkte)
b) Entwerfen Sie eine Maschine, die als Schwarzer
gewinnt.
(4 Punkte)
c) Wählen Sie eine Kodierung der
Eingabe/Ausgabe/Zustand.
Beachten Sie dabei, daß nur die in obiger Stellung beim
Algorithmus
aus a) möglichen Züge kodiert zu werden brauchen, nicht
beliebige
Züge in einem Schachspiel. (2 Punkte)
d) Geben Sie die kodierten Ein und Ausgaben und
Zustände
an, wenn Weiß mit dem Zug Ka2 beginnt und nachfolgend von der
Maschine
matt gesetzt wird. (2 Punkte)
e) Verbessern Sie die Kodierung aus c) zu einem Kode,
der einen Fehler korrigieren kann. Beweis. (3 Punkte)
f) Geben Sie unter Verwendung der Kodierung aus c) die
Booleschen Funktionen für
f: (Zustand, Eingabezeichen) -------> (Nachfolgezustand, Ausgabezeichen)
an (3 Punkte)
g) Wenden Sie das Verfahren von Quine McCluskey an
um
die Booeleschen Funktionen aus f) zu minimieren. (4 Punkte)
h) Zeichnen Sie das Schaltnetz zu den minimierten
Funktionen
aus g) (2 Punkte)