URL:         /axel/informatik1_ws0304_blatt11.html
Dieses  Übungsblatt ist in Zweiergruppen zu bearbeiten. Auf dem Blatt  bitte Übungsgruppentag angeben. Um den Übungsschein zu erhalten, muß man 50% der Punkte erreichen und aktiv am Übungsbetrieb teilnehmen. D.h Vorrechnen, Bearbeitung von mindestens 80% der  Übungsblätter.

Jede Aufgabe auf einem eigenen Blatt (mit Namen und Gruppe und Matrikelnummern). Nicht mit Bleistift bearbeiten.

Aufgabe 31-  Benes  (3+3+2+3+3 Punkte)

a) Man berechne für das Benes Permutationsnetz mit 2n Eingängen die Anzahl der möglichen Kombinationen von Schalterstellungen.
b) Zeigen Sie, daß diese Anzahl für Netze mit mehr als zwei Eingängen größer ist als die Anzahl der möglichen Permutationen der Eingabedaten.
c) Wieviele Schritte sind beim Benes Netz mit m = 2n Prozessoren höchstens nötig, um eine Information vom Prozessor i zu einem Prozessor j zu senden. Die vorherige Berechnung der Schalterstellung bleibt dabei unberücksichtigt.
d) Sei ein 8 Prozessor Netzwerk gegeben. Die Prozessoren seien über ein Benes Netz verbunden. Die Daten aus Prozessor 1 sollen zum Prozessor 6 (1->6) die weiteren Zuordungen seien (2->3, 3->8, 4->5, 5->1, 6->7, 7->2, 8->4). Man zeichne das Benes Permutationsnetz und berechne eine Schalterstellung zur Realisierung dieser Permutation.
e) Man gebe eine 8 stellige Permutation und zwei verschiedene Schalterstellungen an, die diese Permutation realisieren.
 

Aufgabe 32 -Würfel (4+2 Punkte)

 
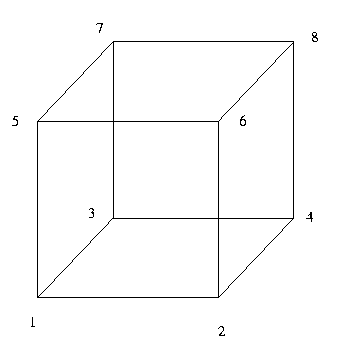
  Realisieren Sie die Permutation aus 31d auf einem dreidimensionalen Würfel:

Dabei kann in einem Schritt entlang einer Kante   nur eine Information weitergegeben werden. In einem Knoten können genau 2  Datensätze gespeichert werden.  Versuchen Sie mit möglichst wenigen Schritten auszukommen. Beweisen Sie die Minimalität Ihrer Lösung (2 Punkte)