Prof. Dr. R.
Laue
WS0304
Informatik I
Übungsblatt 1
Abgabe: 06.11. vor der Vorlesung
URL:
/axel/informatik1_ws0304_blatt1.html
Dieses Übungsblatt ist in Zweiergruppen zu
bearbeiten. Auf dem Blatt bitte Übungsgruppentag angeben. Um
den Übungsschein zu erhalten, muß man 50% der Punkte
erreichen
und aktiv am Übungsbetrieb teilnehmen. D.h Vorrechnen, Bearbeitung
von mindestens 80% der Übungsblätter.
Die
Übungen finden erstmalig am 29.10. und 30.10. statt.
Jede Aufgabe auf einem eigenen Blatt (mit Namen und Gruppe und
Matrikelnummern).
Aufgabe 1 - Kassenmaschine - (4 Punkte)- eigenes Blatt
Man definiere eine endliche Maschine (d.h.
Angabe des
6 Tupels), die bei Einwurf von Münzen (0.5 Euro, 1 Euro, 2 Euro, 5
Euro) in beliebiger Reihenfolge anzeigt, welcher Betrag noch
eingeworfen
werden muß um 7.5 Euro zu erreichen, bzw bei Erreichen von
7.5 Euro Einlaß
gewährt. Es soll keine Rückgabe von Geld erfolgen. Man
berücksichtige
auch das Problem, wie die Maschine merkt, daß ein neuer Mensch
Einlaß
begehrt.
Man ändere obige Maschine in eine
Maschine, die außerdem ausländische Euro-Münzen klaut:
Handelt es sich um eine ausländische Euro-Münze wird diese
einfach geschluckt . (2 Extrapunkte)
Aufgabe 2 - Addierer - (2+4 Punkte)- eigenes Blatt
Zeichnen Sie die Folge der
Zustände und die
Ausgabe
bei der binären Addition von 111100110 = 0*20 + 1*21
+ 1+22 + 0*2^3 ... und 101101001 mit Hilfe des in der
Vorlesung
definierten binären Addierwerks. Geben Sie diese Definition mit
an.
Was ist der erreichte Zustand?
Analog zum binären Addierwerk
kann man
ein
Addierwerk
zur Addition von zwei Zahlen im Ternärsystem definieren. Geben Sie
eine Definition an und führen Sie eine Beispieladdition mit Ihren
beiden Matrikelnummern modulo 1000 im Ternärsystem durch.
Verwenden Sie dazu ihre definierte Maschine.
Aufgabe 3 - Übergangsgraph, Erkennen von Sprachen- (3+3+2
Punkte)- eigenes Blatt
1) Geben Sie einen endlichen Automaten an
, der die
Sprache
L = { ca3b3bmcna2
| n>=0 , m>=0 } hat. D.h. nach Eingabe eines Wortes der Sprache
soll der
Automat in einem Zustand aus der Menge der Endzustände sein.
Zeichnen
Sie den Übergangsgraph.
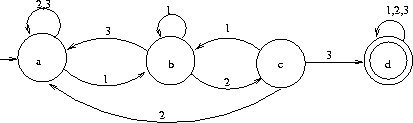
2)Gegeben sei der folgende
Übergangsgraph
Hierbei
wurde die
übliche Notation verwendet:
unbeschrifteter Eingangspfeil am Startzustand, Doppelkreise bei der
Finalmenge. Definieren Sie den zugehörigen endlichen Automaten
(mathematisch korrekte als Tupel) (1 Punkt), was
ist die akzeptierte Sprache? (sprachlich, nicht unbedingt als
Formel)
(2 Punkte)
3)Entwerfen Sie einen Automaten, dessen Sprache
die Wörter aus a,b und c sind, wobei die Anzahl der a durch drei
teilbar ist.