Prof. Dr. R. Laue
WS0001
Informatik I
Übungsblatt 2
Abgabe: 2.11.00 vor der Vorlesung
URL: /axel/informatik1_ws0001_blatt2.html
Dieses Übungsblatt ist in Zweiergruppen zu
bearbeiten. Auf dem Blatt bitte Übungsgruppentag angeben. Um
den Übungsschein zu erhalten muß man 50% der Punkte erreichen
und zweimal erfolgreich eine Aufgabe vorrechnen.
Aufgabe 4 - Schubfachprinzip - (4 Punkte)
Zeigen Sie, daß es keinen endlichen Automaten mit
dem Eingabealphabet 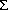 = {( ,) ,x} gibt, der die Sprache
= {( ,) ,x} gibt, der die Sprache
L = { (n x )n | n>0 }
akzeptiert. Hinweis: Wenden Sie das Schubfachprinzip auf
die Menge der Zustände an.
Schubfachprinzip: Hat man m>n Dinge in n Schubfächern,
so gibt es ein Schubfach mit mindestens 2 Dingen.
Aufgabe 5 - Jahreszahlenerkenner - (4+3 Punkte)
Geben Sie den Übergangsgraphen zu einem endlichen Automaten,
der gültige Jahreszahlen erkennen soll an. D.h. das Eingabealphabet
besteht aus den Ziffern 0,1,2,..,9 und dem Sonderzeichen #, welches ein
beliebiges anderes Zeichen kodiert. Die Ziffernfolge zwischen dem
Sonderzeichen # wird als Jahreszahl interpretiert. Liegt diese Zahl zwischen
1 und 2000 soll der Automat in einem Zustand aus der
Endzustandsmenge wechseln und im weiteren in diesem verbleiben. Beispiel: #345#
ist o.k. 123 ist ok 123454# ist nicht
o.k. ###11# ist ok #001# ist ok #0000#2222# ist nicht o.k.
Schreiben Sie das zugehörige 5 Tupel auf.
Aufgabe 6 - Komposition von Maschinen - (2+2+2+2 Punkte)
In der Vorlesung wurde skizziert, wie man eine endliche Maschine zur
parallelen Addition von mehreren k-stelligen Zahlen entwirft.
a) Zeichnen Sie das Blockschaltbild der endlichen Maschine
zur parallelen Addition von 16 Zahlen
b) Wieviel Takte benötigt man zur parallelen Addition
von 1048576 k-stelligen Zahlen? Ein Takt ist dabei ein Übergang (d.h.
Einlesen, Zustandwechsel) in der zugrunde liegenden Gesamtmaschine.
c) Wieviele Addierer sind in dem Schaltnetz aus b)
?
d) Wieviele verschiedene Zustände hat die Maschine aus
b) ?
![]() = {( ,) ,x} gibt, der die Sprache
= {( ,) ,x} gibt, der die Sprache