Complete monomial groups
We have already met the wreath product H wr X G , where G is
a group acting on X while H acts on Y. Now we
consider the particular case where G is a permutation group, say
G <= S n , and where we take for GX the natural action of G on n.
In this case we shorten the notation by putting
H wr G:=H wr n G.
A particular case is H wr S n , the complete monomial group
of degree n over H. Many important groups are of this form, examples will
be given in a moment. In the case when
H <= S m , then H wr G has the following natural embedding
into S mn :
d: S m wr S n hookrightarrow S mn
where (y,p) is mapped onto the permutation given by
(j-1)m+i -> ( pj-1)m+ y( pj)i " i Îm,j În.
This can be seen as follows:
Remember the direct factors S m j, for j În, of the base
group S m * of S m wr S n (cf. the remark on Hx
in the Lemma). Its image d[ S m j] acts on the block
{(j-1)m+1, ...,
jm } as S m does on m, while the image d[ S n ']
of the complement S n ' of the base group acts on the set of
these n subsections {(j-1)m+1, ...,jm } of length m
of the set mn
as S n does act on n. For example the
element
( y, p):=( y(1), y(2), y(3), p):=((12),(123),1,
(23)) ÎS 3 wr S 3
is mapped under d onto
(12)(456) (47)(58)(69) =(12)(475869) ÎS 9,
where (12)(456)= d(( y,1)) and (47)(58)(69)= d(( i, p)).
The image of H wr G under d will be denoted as follows:
H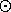 
G:= d[H wr G].
It is called the plethysm
of G and H, for reasons which will become clear later.
harald.fripertinger@kfunigraz.ac.at,
last changed: August 28, 2001
