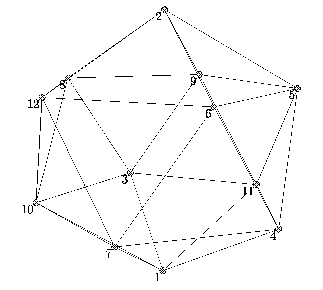

The orbits of {1, 2, 3, 4, 5, 7}, {1, 3, 4, 7, 10, 11} and {1, 4, 5, 7, 9, 10} under A form the blocks of the M12-design. The stabilizer of first two sets in A is trivial, the third is of order five, generated by x. The orbits are thus of length 60, 12 and 60 respectively.
|
|
|
|
|
|
|
Let i=1,...12 denote the elements of the projective line over GF(11), where we identify < (1,i) > with i , i=1,...,10 and put < (1,0) > = 11 and < (0,1) > = 12.
The matrices
6 0 0 2and
1 9 5 2induce the given generators x and y on the projective line. Thus, we embed A into PSL(2,11). The three orbits indicated above fuse into one orbit of length 132 under PSL(2,11). The element x generates the stabilizer of {1, 3, 4, 7, 10, 11} in PSL(2,11), too.
Back to the
DISCRETA homepage.
Last updated: September 17, 1999, Anton Betten