Führen Sie am folgenden Beispiel die Berechnung der starken Zusammenhangskomponenten durch.
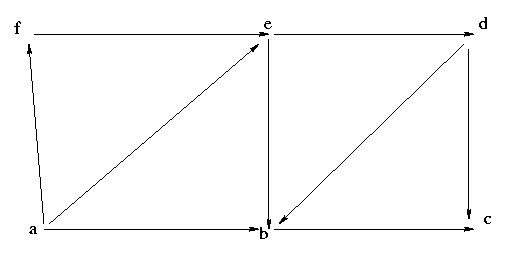
Stellen Sie den jeweiligen Kellerinhalt dar.
URL: /axel/graph_ws0001_blatt6.html
Führen Sie am folgenden Beispiel die Berechnung der starken
Zusammenhangskomponenten durch.
Stellen Sie den jeweiligen Kellerinhalt dar.
Auf unserem Weg zum Algorithmus für bcc definieren wir:
Das Zentrum der bcc sei der Knoten mit der zweitkleinsten DFSNUM. Bei Verwendung der Notation (T,F,B,DFSNUM, FATHER) aus dem DFS Algorithmus definiert man ähnlich wie bei der Einfachzusammenhangskomponente:
LOWPT[v]= min { DFSNUM[v] ![]() {DFSNUM[z] | ex ein Knoten w mit v --T*> w
--B> z}}
{DFSNUM[z] | ex ein Knoten w mit v --T*> w
--B> z}}
Beweisen Sie folgendes Lemma:
1) LOWPT[v] <= DFSNUM[FATHER[v]] für alle v mit DFSNUM[v] >=2
2) v ist Zentrum einer bcc <==> LOWPT[v] = DFSNUM[FATHER[v]]
und DFSNUM[v] >= 2