oder: int demoucron_extd(int *graph, int **faces)
- Zweifach zusammenhängender (biconnected) Graph ohne Selbstschleife (self-loop) in Form einer Nachbarschaftsliste
- Zweifach zusammenhängender (biconnected) Graph ohne Selbstschleife (self-loop) in Form einer Nachbarschaftsliste
- Adresse eines Integerzeigers
- 0, falls der übergebene Graph nicht planar ist
- 1, falls der übergebene Graph planar ist
- -1 im Fehlerfall: "Es wurde kein Zyklus gefunden" (kann bei zweifach zusammenhängenden Graphen jedoch nicht passieren!)
Der Algorithmus führt dabei folgende Schritte durch:
Sei G der übergebene zweifach zusammenhängende Graph ohne Selbstschleife:
- Suche einen Zyklus G'
- Berechne alle Fragmente aus G\G'
- Falls keine Fragmente vorhanden: G ist planar, Ende.
- Berechne alle Flächen
- Berechne die "admissible faces" für jedes Fragment
- Wenn es ein Fragment ohne "admissible face" gibt: G ist nicht planar, Ende.
- Wähle einen alpha-Pfad aus dem Fragment mit der geringsten Anzahl an 'admissible faces' und bette ihn in G' ein bzw. entferne ihn aus G, gehe zu (2.)
In jedem Fall muss der übergebene Graph zweifach zusammenhängend sein und darf keine Selbstschleifen besitzen. Erfüllt der übergebene Graph wenigstens eines dieser beiden Kriterien nicht, so kann der Programmaufruf zu einem Absturz führen.
Graph G(7):
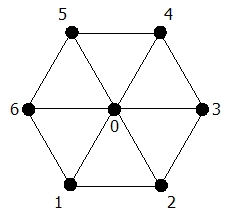Abb.: Graph G(7)Ein solcher Graph kann mittels constructG(n) für allgemeine n erzeugt werden. Die Prozedur constructG(int n) erwartet eine ganze Zahl n > 3. Sie konstruiert einen Graph mit n Knoten, in dem die Knoten 1 bis n zyklisch verkettet sind, und der Knoten 0 mit jedem dieser Knoten verbunden ist. Als Rückgabe hat sie den entsprechenden Graphen G(n) in Form einer Nachbarschaftsliste, also vom Typ int *graph
Hier lautet die Nachbarschaftsliste entsprechend:
8 14 17 20 23 26 29 32 1 2 3 4 5 6 0 6 2 0 1 3 0 2 4 0 3 5 0 4 6 0 5 1
Bei Aufruf von demoucron(constructG(7)) beispielsweise liefert die Prozedur als Rückgabewert 1, da der Graph planar ist.
Bei Aufruf von demoucron_extd(constructG(7), &faces) mit einem zusätzlichen Parameter vom Typ int *faces werden die Flächen zusätzlich in einem Array mit der Startadresse &faces gespeichert und zwar in der folgenden Form:
Das Array hat nach Aufruf von demoucron_extd(constructG(7), &faces) folgende Einträge:
6 5 4 3 2 1 -1 3 2 0 -1 2 0 1 -1 0 6 1 -1 0 5 6 -1 0 4 5 -1 0 3 4 -2
Die einzelnen Flächen sind also durch eine -1 abgetrennt. Eine -2 gibt schließlich das Arrayende an.
Graph K(3,3):
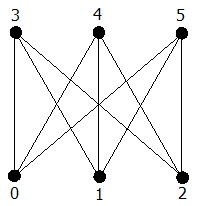Abb.: Graph K(3,3)Ein solcher Graph kann mittels constructK(n,m) für allgemeine n erzeugt werden. Die Prozedur constructK(int n, int m) erwartet zwei ganze Zahlen n > 1, m > 1. Sie konstruiert einen Graphen mit n+m-Knoten, in dem die ersten n genau mit den letzten m-Knoten verbunden sind. Als Rückgabe hat sie den entsprechenden Graphen K(n,m) in Form einer Nachbarschaftsliste, also vom Typ int *graph
Hier lautet die Nachbarschaftsliste demnach:
7 10 13 16 19 22 25 3 4 5 3 4 5 3 4 5 0 1 2 0 1 2 0 1 2
Bei Aufruf von demoucron(constructK(3,3)) beispielsweise liefert die Prozedur als Rückgabewert 0, da der Graph nicht planar ist.
Bei Aufruf von demoucron_extd(constructK(3,3), &faces) wird ebenfalls eine 0 zurückgegeben und das Array mit der Startadresse &faces hat nachher lediglich als einzigen Eintrag:
-2